K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KC
1
4 tháng 10 2021
\(\left(x+4\right)\left(x^2-4x+16\right)-x\left(x-5\right)\left(x+5\right)=264\)
\(\Leftrightarrow x^3+64-x^3+25x=264\)
\(\Leftrightarrow25x=200\)
hay x=8
8 tháng 10 2021
\(=\left(x^3-2x^2+x+2x^2-4x+2-2x+7\right):\left(x^2-2x+1\right)\\ =\left[\left(x^2-2x+1\right)\left(x+2\right)-2x+7\right]:\left(x^2-2x+1\right)\\ =x+2\left(dư:-2x+7\right)\)
DL
0
CU
15 tháng 7 2019
a, 3x2 - 8x + 4
= 3x2 - 6x - 2x + 4
= 3x(x - 2) - 2(x - 2)
= (3x - 2)(x - 2)
b, x2 - 4xy + 3y2
= x2 - xy - 3xy + 3y2
= x(x - y) - 3y(x - y)
= (x - 3y)(x - y)
15 tháng 7 2019
\(a)3x^2-8x+4=3x^2-6x-2x+4=3x\left(x-2\right)-2\left(x-2\right)=\left(3x-2\right)\left(x-2\right)\)
\(b)x^2-4xy+3y^2=x^2-xy-3xy+3y^2=x\left(x-y\right)-3y\left(x-y\right)=\left(x-3y\right)\left(x-y\right)\)
\(c)2x^2+3881x-17505=2x^2+3890x-9x-17505=2x\left(x+1945\right)-9\left(x+1945\right)\)
\(=\left(2x-9\right)\left(x+1945\right)\)
4 tháng 10 2021
Bài 3:
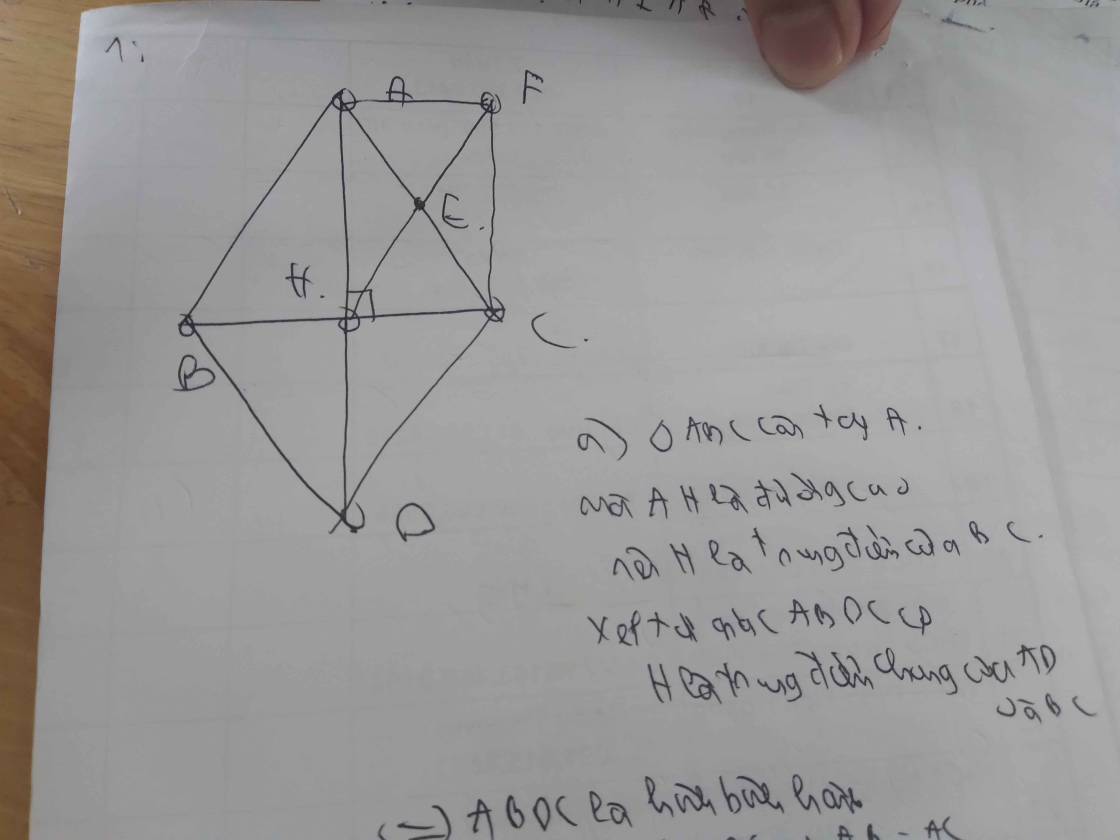
b: Xét ΔABC có
I là trung điểm của BC
IK//AC
Do đó: K là trung điểm của AB
Xét ΔABC có
I là trung điểm của BC
IH//AB
Do đó: H là trung điểm của AC
Xét ΔABC có
K là trung điểm của AB
H là trung điểm của AC
Do đó: HK là đường trung bình của ΔABC
Suy ra: HK//BC
13 tháng 12 2021
\(a,\dfrac{11x}{2x-5}+\dfrac{x-30}{2x-5}=\dfrac{11x+x-30}{2x-5}=\dfrac{12x-30}{2x-5}=\dfrac{6\left(2x-5\right)}{2x-5}=6\)
\(b,\dfrac{3x^2-1}{2x}+\dfrac{x^2+1}{2x}=\dfrac{3x^2-1+x^2+1}{2x}=\dfrac{4x^2}{2x}=2x\)
\(c,\dfrac{3}{2x-5}+\dfrac{-2}{2x+5}+\dfrac{-20}{4x^2-25}=\dfrac{3\left(2x+5\right)}{\left(2x-5\right)\left(2x+5\right)}-\dfrac{2\left(2x-5\right)}{\left(2x-5\right)\left(2x+5\right)}-\dfrac{20}{\left(2x-5\right)\left(2x+5\right)}=\dfrac{6x+15-4x+10-20}{\left(2x-5\right)\left(2x+5\right)}=\dfrac{2x+5}{\left(2x-5\right)\left(2x+5\right)}=\dfrac{1}{2x-5}\)
\(d,\dfrac{x-2}{x-1}+\dfrac{x-3}{x+1}+\dfrac{4-2x^2}{x^2-1}=\dfrac{\left(x-2\right)\left(x+1\right)+\left(x-3\right)\left(x-1\right)+4-2x^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2-2x+x-2+x^2-3x-x+3+4-2x^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{-5x+5}{\left(x-1\right)\left(x+1\right)}=\dfrac{-5\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{-5}{x-1}\)
\(e,\dfrac{x+1}{x-1}+\dfrac{1-x}{x+1}+\dfrac{4}{x^2-1}=\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}-\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}+\dfrac{4}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2+2x+1-x^2+2x-1+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{4\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{x-1}\)
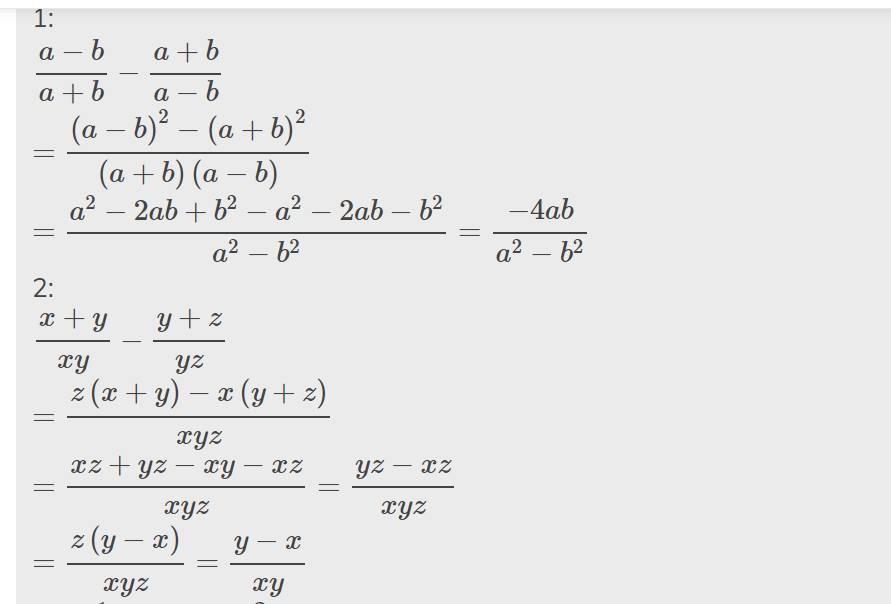
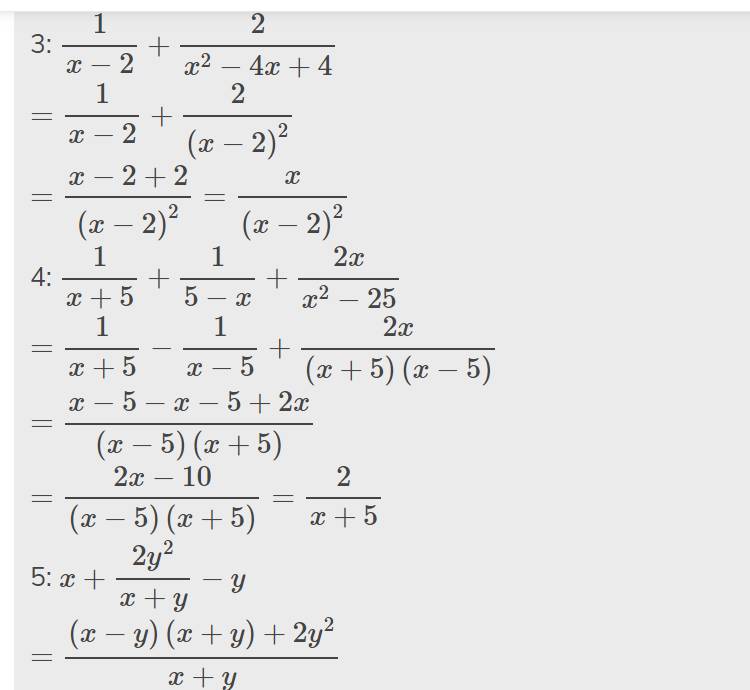
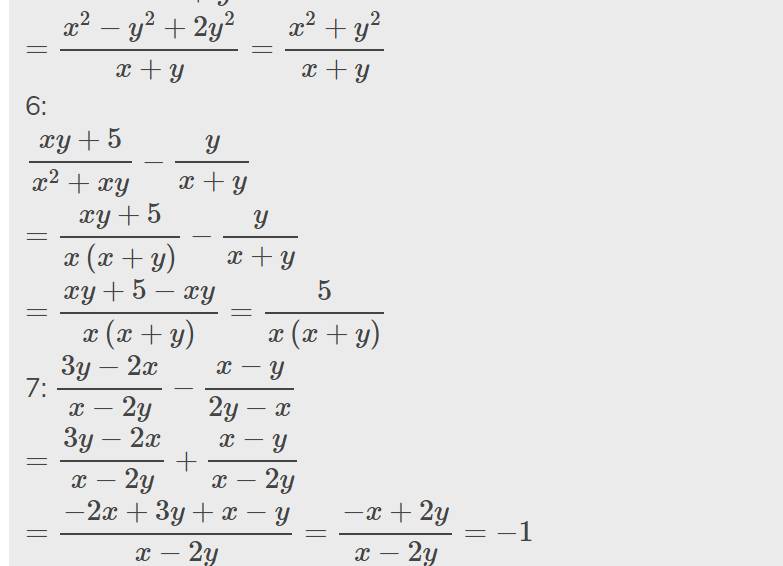
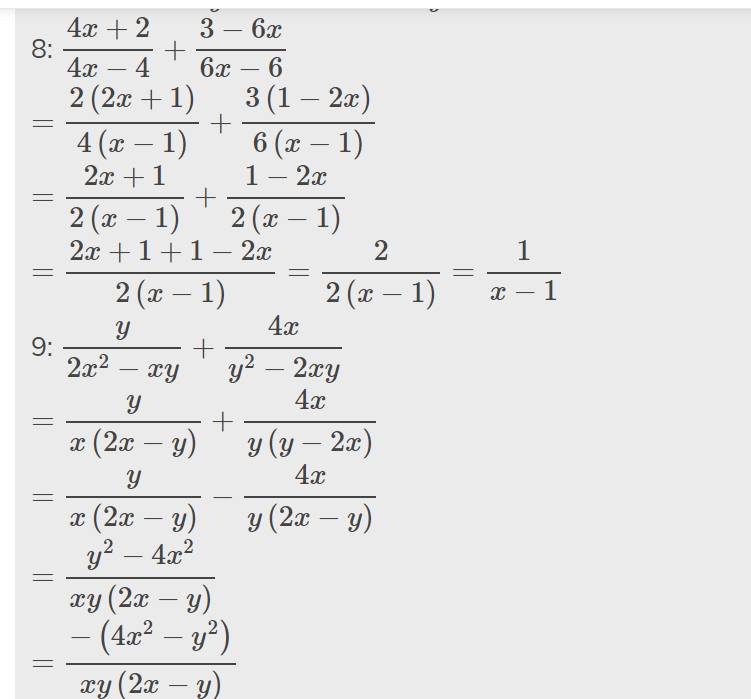
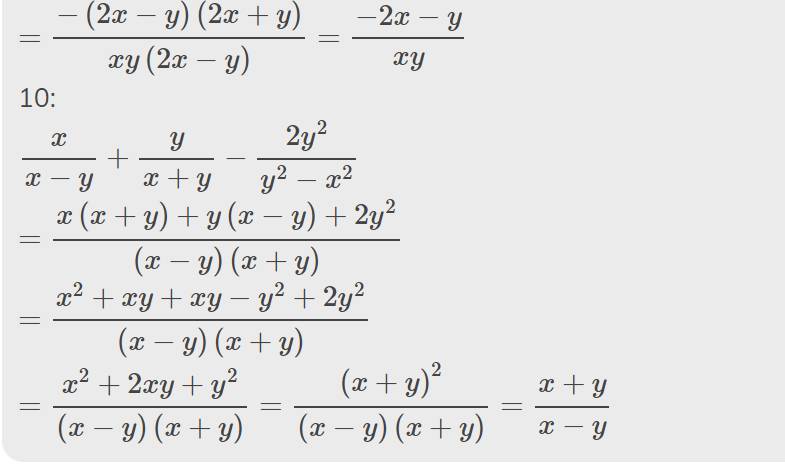
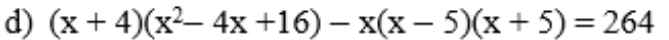
\(\Leftrightarrow18x^2\left(x+4\right)-12x\left(x+4\right)=0\)
\(\Leftrightarrow6x\left(x+4\right)\left[3x-2\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+4=0\\3x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-4\\x=\dfrac{2}{3}\end{matrix}\right.\)
⇔18x2(x+4)−12x(x+4)=0⇔18x2(x+4)−12x(x+4)=0
⇔6x(x+4)[3x−2]=0⇔6x(x+4)[3x−2]=0
⇔⎡⎢⎣x=0x+4=03x−2=0⇔[x=0x+4=03x−2=0
⇔⎡⎢ ⎢ ⎢⎣x=0x=−4x=23