Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
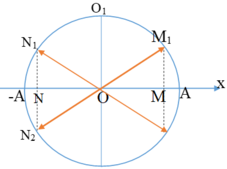
+ Cứ sau 0,05s chất điểm lại đi qua các điểm M, O và N
![]()
+ Từ hình vẽ, ta thấy rằng:
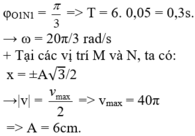

Đáp án B
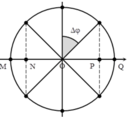
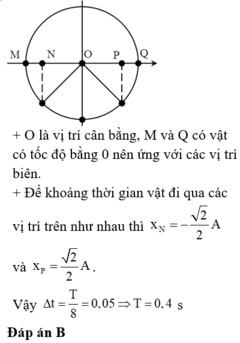
+ O là vị trí cân bằng, M và Q có vật có tốc độ bằng 0 nên ứng với các vị trí biên.
+ Để khoảng thời gian vật đi qua các vị trí trên như nhau thì
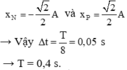

ta có : cứ 0,25s thì qua M,N,O nên trong một chu kì chia ra 6 đoạn->T/6=0,25s suy ra T=1,5s
\(\left|xM\right|\)=\(\left|xN\right|\)=\(\frac{A\sqrt{3}}{2}\) (từ cân bằng ra M là T/6 nên x=\(\frac{A\sqrt{3}}{2}\))
\(\left|vM\right|\)=\(\left|vN\right|\)=\(\frac{Vmax}{2}\)
12 căn 3 pi=0,5.A.\(\frac{2pi}{T}\)->A=18\(\sqrt{3}\) cm

Đáp án A
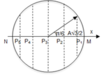
Chất điểm chuyển động chia đường tròn thành 12 cung, thời gian chuyển động trên mỗi cung tròn là 0,25 s.
→ chu kì dao động của chất điểm là T = 12.t = 12.0,25 = 3 s.
→ tần số góc ω = 2π/3 rad/s.
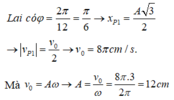

chọn đáp án D
Xét khoảng cách từ một điểm tới nút gần nhất có khoảng cách là d( với
d
<
λ
4
)
ta có •
d
=
λ
12
thì biên độ dao động tại điểm đó là
A
2
•
d
=
λ
8
thì biên đọ dao động tại điểm đó là
A
2
2
d
=
λ
6
thì biên độ tại điểm đó là
A
3
2
Với A là biên độ dao động tại bụng sóng
►Đây là tb tự luận :P
Xét ba điểm M N P liên tiếp nhau trên một sợi dây mang sóng dừng
Ta có M và N dao động ngược pha nhau nên M và N đối xứng nhau qua một nút
M,N, P là ba điểm liên tiếp cùng biên độ nên ta có N và P đối xứng nhau qua một bụng
Biểu diễn trên hình ta có
M
N
2
+
N
P
2
=
λ
4
⇒
λ
=
6
c
m
GỌi M và N đối xứng nhau qua nút O
Xét Pt sóng tới O
u
1
=
A
cos
(
ω
t
)
Sóng phản xạ tại O
u
2
=
A
cos
(
ω
t
+
π
)
Xét tại điểm N
=
2
A
cos
(
π
2
+
2
π
O
N
λ
)
cos
(
ω
t
+
π
2
)
Biên độ sóng tại N
A
N
=
2
A
/
cos
(
π
2
+
2
π
O
N
λ
)
/
⇒
2
A
=
8
c
m
Như vậy biên độ tại bụng là 8 mm
Khoảng thời gian giữa hai lần sợi dây duỗi thẳng là
T
2
=
0
,
04
⇒
T
=
0
,
4
s
Vận tốc cực đại của phần tử tại bụng sóng
v
=
A
ω
=
A
2
π
T
=
628
m
m
/
s

Từ đề bài ta suy ra M và N là vị trí có li độ \(\frac{\left|A\right|\sqrt{3}}{2}\)
\(\rightarrow\frac{T}{6}=0,05s\rightarrow T=0,3s\)
Ta có :
\(\upsilon=\frac{\upsilon_{max}}{2}\rightarrow\upsilon_{max}=40\pi\left(cm\text{ / s }\right)\rightarrow A\text{ω }=A.\frac{2\pi}{T}=40\pi\)
→ A = 6cm


A/ Nê-grô-it