Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D

+ T = 1s => ω = 2π rad/s.
+ Độ biến dạng của lò xo ở vị trí cân bằng:
![]()
+ Biên độ dao động:
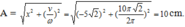
+ Thời điểm t = 0 tương ứng với một gốc lùi Δφ = ωt = 2π.2,5 = 5π trên đường tròn.
+ Lực đàn hồi khi đó có độ lớn:
Fđh = k(Δlo + x) = k(25 + 5√2). 10-2 N.
Kết hợp với Fđhmin = k.(Δlo - A) = k. 15.10-2 = 6N.
+ Từ hai biểu thức trên ta thu được Fđh = 12,82N.

Đáp án C

Vận tốc cực đại của dao động a m a x = ω A = 4 π cm / s
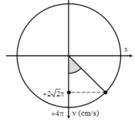
Tại thời điểm t = 0,25 s vật có vận tốc v = 2 2 x m a x = 2 π 2 cm / s
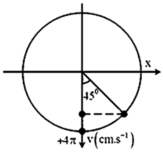
Tại thời điểm t=0 ứng với góc lùi ∆ φ = ω ∆ t = 0 , 25 π
Biễu diễn các vị trí tương ứng trên đường tròn. Ta thu được φ 0 = - π 2 r a d
Phương trình dao động của vật là x = 4 cos ( πt - π 2 ) c m

Chọn đáp án C
Vận tốc cực đại của dao động:
v max = ω A = 4 π c m / s .
Tại thời điểm t = 0,25 s vật có vận tốc:
v = 2 2 v max = 2 π 2 c m / s .
Biễu diễn các vị trí tương ứng trên đường tròn.
Ta thu được: φ 0 = − π 2 r a d .
Phương trình dao động của vật là:
x = 4 cos π t − π 2 c m .

a) \(v_{max}=\omega.A\Rightarrow \omega=\dfrac{10\pi}{5}=2\pi(rad/s)\)
Vậy PT dao động là: \(x=5\cos(2\pi t+\dfrac{\pi}{3})cm\)
b) Áp dụng CT độc lập:
\(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow 5^2=3^2+\dfrac{v^2}{(2\pi)^2}\)
\(\Rightarrow v=\pm 8\pi(cm/s)\)

+ Vận tốc cực đại của dao động amax = ωA = 4π cm/s.
+ Tại thời điểm t = 0,25 vật có vận tốc
v = 2 2 v m a x = 2 π 2 cm/s
Thời điểm t = 0 ứng với góc lùi Δφ = ωΔt = 0,25π.
Biểu diễn các vị trí tương ứng trên đường tròn. Ta thu được: φ 0 = - π 2 rad
+ Phương trình dao động của vật
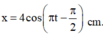
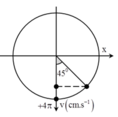
Đáp án C




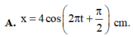
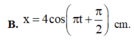
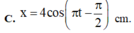
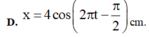

a