Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: Chiều dài từ gốc cây đến chỗ cây bị gãy là 3m
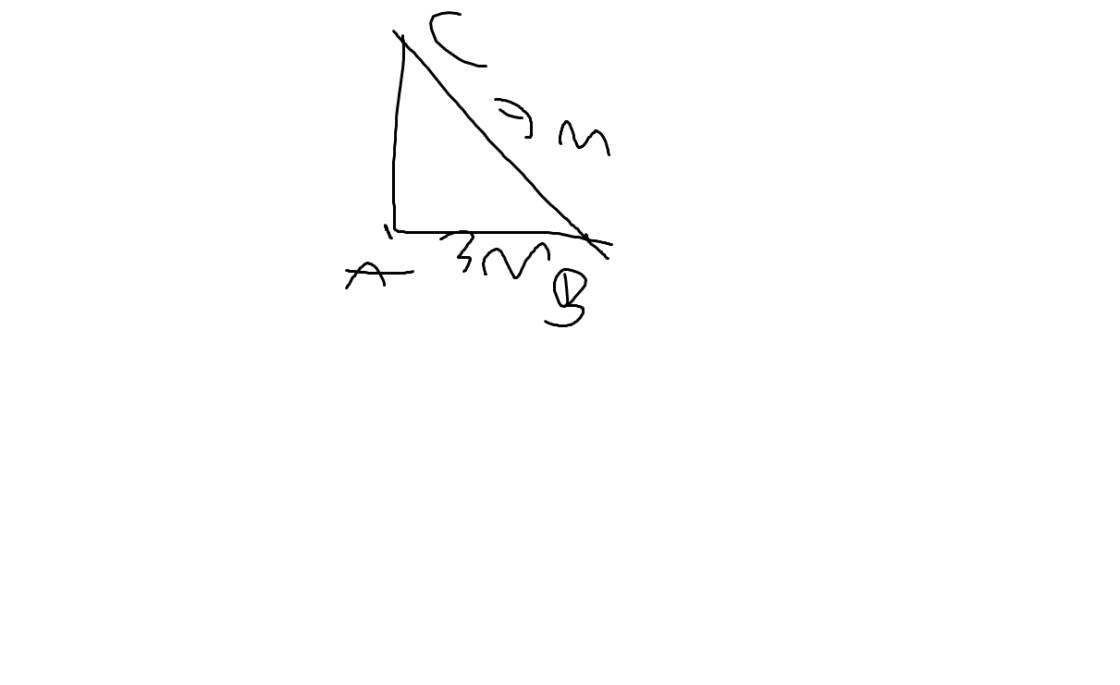
Gọi A là gốc của cái cây
Gọi Clà ngọn của cái cây
Gọi B là chỗ cây bị gãy
Do đó, ta có: \(AB\perp AC\)
Theo đề, ta có: BC=7m; AB=3m
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{7^2-3^2}=2\sqrt{10}\left(m\right)\simeq6,3\left(m\right)\)

Áp dụng đ/l Pytago vào tam giác vuông ABC, có :
\(BC^2=AB^2+AC^2\\ \Rightarrow AC^2=BC^2-AB^2\\ \Rightarrow AC=\sqrt{4^2-3^2}\\ =\sqrt{7}\left(m\right)\)
Chiều cao của cây lúc chưa gãy là :
\(4+\sqrt{7}\approx6,6\left(m\right)\)
A B C 4 3
Áp dụng định lý Pytago cho tam giác ABC ta có:
\(AB^2+AC^2=BC^2\)
Thay số: \(3^2+4^2=BC^2\)
\(BC^2=25 \)
\(BC=5\)
Vậy chiều cao của cái cây lúc chưa bị gãy là:
\(5 +4 = 9m\)

Lời giải
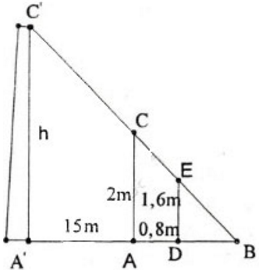
Gọi chiều cao của cây là h = A'C' và chọn một cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Giải:
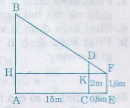
Giả sử AB là cây cần do, CD là cọc EF là khoảng cách từ mắt tới chân.
∆KDF ∽ ∆HBF
=> HBKD=HFKFHBKD=HFKF
=> HB = HF.KDKFHF.KDKF
mà HF = HK + KF =AC + CE = 15 + 0,8 = 15.8m
KD = CD - CK = CD - EF = 2 - 1,6 = 0,4 m
Do đó: HB = 7,9 m
Vậy chiều cao của cây là 7,9 m.

Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB 
Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB 
Vậy cây cao 9,5m.

C' A' A D B C E 2m 1,6m 15m 0,5m
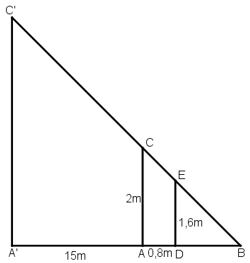
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB 
\(\Rightarrow\frac{DE}{AC}=\frac{DB}{AB}\)
Mà AC = 2m , DE = 1,6m
nên \(\frac{1,6}{2}=\frac{DB}{AB}\Rightarrow\frac{DB}{AB}=\frac{4}{5}\Rightarrow\frac{DB}{4}=\frac{AB}{5}\)
Áp dụng t/c DTSBN , ta có:
\(\frac{DB}{4}=\frac{AB}{5}=\frac{AB-DB}{5-4}=\frac{AD}{1}=0,8\)
Suy ra :
\(\frac{DB}{4}=0,8\Rightarrow DB=0,8.4=3,2\)
\(\frac{AB}{5}=0,8\Rightarrow AB=0,8.5=4\)
Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB ~ ΔA’C’B (vì AC // A’C’)
\(\Rightarrow\frac{AB}{A'B'}=\frac{AC}{A'C'}\)
\(\Rightarrow AC=\frac{AC.A'B'}{AB}=\frac{2.19}{4}=9,5\left(m\right)\)
Vậy cây cao 9,5m



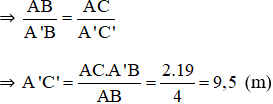
Phần gãy dài \(\sqrt{6^2+8^2}=10(m)\)
Vậy cây cao \(10+6=16(m)\)