Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Số cách chọn 4 học sinh bất kì n ( Ω ) = C 35 4 = 52360 (cách).
Số cách chọn 4 học sinh chỉ có nam hoặc chỉ có nữ là C 20 4 + C 15 4 = 6210 (cách).
Do đó số cách chọn 4 học sinh có cả nam và nữ là n(A) = 52360 - 6210 = 46150 (cách).
Vậy xác suất cần tính là
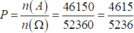

Đáp án A
Ta thấy trong các đối tượng ta cần chọn, thì chỉ có lớp phó phong trào không đòi hỏi điều kiện gì nên ta sẽ chọn ở bước sau cùng
Do đó chọn 1 ban cán sự ta cần thực hiện các bước sau
Bước 1: Chọn1 bạn nữ là lớp trưởng có 15 cách
Bước 2: Chọn 1 bạn nam làm lớp phó học tập có 18 cách
Bước 3: Chọn1 bạn nữ là thủ quỹ có 14 cách
Bước 4: Chọn 1 người trong số còn lại làm lớp phó phong trào có 30 cách
Vậy tất cả có ![]() cách cử 1 ban cán sự
cách cử 1 ban cán sự

Đáp án B
Số phẩn tử không gian mẫu là ![]()
Gọi A là biến cố “Hai học sinh A, B ngồi cạnh nhau”.
Chọn 1 bàn để xếp hai học sinh A, B có 15 cách.
Xếp A, B ngổi vào bàn được chọn có 2! cách.
Xếp 28 học sinh còn lại có 28! cách.
Vậy ![]()
Do đó ![]()

\(\Omega=C^2_{52}.C^2_{52}\)
a) Trong mỗi bộ có 4 lá K nên số trường hợp rút được 2 K là \(C^2_4\)
\(\Rightarrow P=\frac{C_4^2.C_4^2}{C_{52}^2.C_{52}^2}=\frac{1}{48841}\)
b) Vì bích, rô , nhép, cơ mỗi bộ có 13 lá nên số trường hợp rút được 1 lá mỗi loại là: \(\left(C_{13}^1\right)^4\)
Vì mỗi bộ chỉ được rút 2 lá nên nếu bộ 1 rút được 2 nguyên tố này thì bộ 2 phải rút được 2 nguyên tố kia
---> Số trường hợp bốc được: \(C_4^2\)
\(\Rightarrow P=\frac{C_4^2.\left(C_{13}^1\right)^4}{\left(C_{52}^2\right)^2}=\frac{169}{1374}\)
c) Nếu bộ 1 bốc được 2 con Q nguyên tố này thì 2 con Q của các nguyên tố còn lại phải nằm ở bộ 2
---> Số trường hợp bốc: \(C_4^2\)
\(\Rightarrow P=\frac{C_4^2}{\left(C_{52}^2\right)^2}=\frac{1}{293046}\)
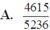
dể thấy : số cách sắp xếp để 2 học sinh \(A;B\) ngồi cùng bàn là : \(30\)
số cách sắp xếp chổ ngồi cho 2 bạn \(A;B\) là \(C^2_{30}=435\)
\(\Rightarrow\) sác xuất để hai học sinh \(A;B\) ngồi cùng bàn là \(P=\dfrac{\left|\Omega_A\right|}{\left|\Omega\right|}=\dfrac{30}{435}=\dfrac{2}{29}\)