Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

dể thấy : số cách sắp xếp để 2 học sinh \(A;B\) ngồi cùng bàn là : \(30\)
số cách sắp xếp chổ ngồi cho 2 bạn \(A;B\) là \(C^2_{30}=435\)
\(\Rightarrow\) sác xuất để hai học sinh \(A;B\) ngồi cùng bàn là \(P=\dfrac{\left|\Omega_A\right|}{\left|\Omega\right|}=\dfrac{30}{435}=\dfrac{2}{29}\)

Đáp án A
Số cách chọn 4 học sinh bất kì n ( Ω ) = C 35 4 = 52360 (cách).
Số cách chọn 4 học sinh chỉ có nam hoặc chỉ có nữ là C 20 4 + C 15 4 = 6210 (cách).
Do đó số cách chọn 4 học sinh có cả nam và nữ là n(A) = 52360 - 6210 = 46150 (cách).
Vậy xác suất cần tính là
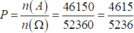

\(\Omega=C^2_{52}.C^2_{52}\)
a) Trong mỗi bộ có 4 lá K nên số trường hợp rút được 2 K là \(C^2_4\)
\(\Rightarrow P=\frac{C_4^2.C_4^2}{C_{52}^2.C_{52}^2}=\frac{1}{48841}\)
b) Vì bích, rô , nhép, cơ mỗi bộ có 13 lá nên số trường hợp rút được 1 lá mỗi loại là: \(\left(C_{13}^1\right)^4\)
Vì mỗi bộ chỉ được rút 2 lá nên nếu bộ 1 rút được 2 nguyên tố này thì bộ 2 phải rút được 2 nguyên tố kia
---> Số trường hợp bốc được: \(C_4^2\)
\(\Rightarrow P=\frac{C_4^2.\left(C_{13}^1\right)^4}{\left(C_{52}^2\right)^2}=\frac{169}{1374}\)
c) Nếu bộ 1 bốc được 2 con Q nguyên tố này thì 2 con Q của các nguyên tố còn lại phải nằm ở bộ 2
---> Số trường hợp bốc: \(C_4^2\)
\(\Rightarrow P=\frac{C_4^2}{\left(C_{52}^2\right)^2}=\frac{1}{293046}\)

Ta đếm số cách chọn 4 học sinh từ đội xung kích mà thuộc cả 3 lớp ở trên.
Phương án 1: Chọn 2 học sinh lớp A, 1 học sinh lớp B và 1 học sinh lớp C.
Số cách chọn trong trường hợp này là ![]() .
.
Phương án 2: Chọn 1 học sinh lớp A, 2 học sinh lớp B và 1 học sinh lớp C.
Số cách chọn trong trường hợp này là ![]() .
.
Phương án 3: Chọn 1 học sinh lớp A, 1 học sinh lớp B và 2 học sinh lớp C.
Số cách chọn trong trường hợp này là ![]() .
.
Theo quy tắc cộng thì số cách chọn 4 học sinh thuộc đủ cả ba lớp là 120 + 90 + 60 = 270.
Trong khi số cách chọn 4 học sinh bất kỳ từ đội xung kích là ![]() .
.
Vậy số cách chọn 4 học sinh mà các học sinh không thuộc quá hai lớp là 495 -270 =225.
Chọn C.

Bạn ơi mình nghĩ bài này phải chia trường hợp ra
VD : TH1: xếp vào tổ 1 : 2 hsg, 2 học sinh khá và 4 học sinh TB thì sẽ có \(C_3^2.C^2_5.C^4_8\) cách chọn
Tương tự các trường hợp còn lại
Mọi người góp ý giúp mình nha
Do ko phân biệt hai tổ (ko cần hoán vị) nên chỉ cần xếp cho 1 tổ, tổ còn lại là phần còn lại (luôn thỏa mãn khi phần 1 thỏa mãn)
Giả sử ta xếp vào tổ có 2 học sinh giỏi \(\Rightarrow C_3^2=3\) cách chọn (1 hsg kết quả cũng vậy)
- Nếu xếp vào 2 hs khá \(\Rightarrow C_5^2=10\) cách chọn
Còn lại 4 bạn trung bình \(\Rightarrow C_8^4=70\)
\(\Rightarrow700\) cách xếp
- Nếu xếp vào 3 hs khá: \(\Rightarrow C_5^3=10\) cách
Còn 3 bạn trung bình: có \(C_8^3=56\) cách
\(\Rightarrow560\) cách
Tổng cộng có: \(3\left(700+560\right)=3780\) cách

Gọi A là tập hợp mọi cách chọn 4 học sinh trong 12 học sinh
Gọi B là tập hợp cách chọn không thỏa mãn yêu cầu đề bài (tức là chọn đủ học sinh 3 lớp)
Gọi C là tập hợp cách chọn thỏa mãn yêu cầu đề bài
Ta có A = B\(\cup\) C, B \(\cap\) C = \(\varnothing\)
Theo quy tắc cộng ta có
\(\left|A\right|\) = \(\left|B\right|\) + \(\left|C\right|\) \(\Rightarrow\) \(\left|C\right|\) = \(\left|A\right|\) - \(\left|B\right|\) (1)
Dễ thấy \(\left|A\right|\) = \(C_{12}^4\) = 495
Để tính \(\left|B\right|\), ta nhận thấy sẽ chọn một lớp có 2 học sinh, còn 2 lớp còn lại mỗi lớp 1 học sinh. Vì thế theo quy tắc cộng và phép nhân, ta có:
\(\left|B\right|\) = \(C_5^2\)\(C_4^1\)\(C_3^1\) + \(C_5^1\)\(C_4^2\)\(C_3^1\) + \(C_5^1\)\(C_4^1\)\(C_3^2\) = 120 + 90 + 60 = 270
Thay vào (1) ta có \(\left|C\right|\) = 495 - 270 = 225
Vậy có 225 cách chọn.
Số cách chọn 4 học sinh từ 12 học sinh đã cho là : C412=495C124=495
Số cách chọn 4 học sinh mà mỗi lớp có ít nhất một em được tính như sau :
* Lớp AA có 2 học sinh, các lớp BB, CC mỗi lớp 1 học sinh.
⇒⇒ Số cách chọn là : C25.C14.C13=120C52.C41.C31=120
* Lớp BB có 2 học sinh, các lớp AA, CC mỗi lớp 1 học sinh.
⇒⇒ Số cách chọn là : C15.C24.C13=90C51.C42.C31=90
Lớp CC có 2 học sinh, các lớp AA, BB mỗi lớp 1 học sinh.
⇒⇒ Số cách chọn là : C15.C14.C23=60C51.C41.C32=60
Số cách chọn 4 học sinh mà mỗi lớp có ít nhất một học sinh là :
120+90+60=270120+90+60=270
Vậy số cách chọn phải tìm là : 495−270=225495−270=225 cách.