Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi phân số cũ là : \(\frac{a}{15}\)
Thì phân số mới là : \(\frac{a-10}{25}\)
Ta có phương trình :
\(\frac{a-10}{25}=\frac{8}{5}.\frac{a}{15}\Leftrightarrow\frac{3a-30}{75}=\frac{8a}{75}\)
\(\Rightarrow3a-30=8a\Leftrightarrow-5a=30\Leftrightarrow x=-6\)
Vậy phân số đó là : \(\frac{-6}{15}=\frac{-2}{5}\)

Gọi phân số cũ là : a/15
Thì phân số mới là : (a-10)/25
Ta có phương trình :
(a-10)/25 = 8/5 . a/15 <=> (3a-30)/75 = 8a/75
=> 3a - 30 = 8a <=> -5a = 30 <=> x = -6
Vậy phân số đó là : -6/15 = -2/5

Khi tử số bớt đi \(9\)đơn vị thì tổng của tử số mới và mẫu số là:
\(128-9=119\)
Nếu tử số mới là \(3\)phần thì mẫu số là \(4\)phần.
Tổng số phần bằng nhau là:
\(3+4=7\)(phần)
Tử số mới là:
\(119\div7\times3=51\)
Tử số là:
\(51+9=60\)
Mẫu số là:
\(128-60=68\)
Phân số cần tìm là: \(\frac{60}{68}\).

Gọi phân số cần tìm là \(\frac{a}{b}\)( \(a\inℤ\); \(b\ne0\))
Theo bài ta có: \(\frac{a}{b}=\frac{3}{5}\)\(\Rightarrow\frac{a}{3}=\frac{b}{5}\)
Đặt \(\frac{a}{3}=\frac{b}{5}=k\left(k\inℕ^∗\right)\)\(\Rightarrow a=3k\); \(b=5k\)
\(\Rightarrow\)Phân số ban đầu có dạng \(\frac{3k}{5k}\)
Nếu cộng thêm 5 vào tử và mẫu thì phân số có giá trị là \(\frac{7}{11}\)
\(\Rightarrow\frac{3k+5}{5k+5}=\frac{7}{11}\)\(\Rightarrow7\left(5k+5\right)=11\left(3k+5\right)\)\(\Rightarrow35k+35=33k+55\)\(\Rightarrow35k-33k=55-35\)\(\Rightarrow2k=20\)\(\Rightarrow k=10\)
\(\Rightarrow a=10.3=30\)và \(b=10.5=50\)
Vậy phân số đã cho ban đầu là \(\frac{30}{50}\)

khi bớt đi 10 đơn vị thì được số đối của nó nên 10 đơn vị là 2 lần mẫu
=>a=5

gọi tử số của phân số là a ; mẫu số của phân số là a+11
Ta có : \(\frac{a+3}{a+11-5}=\frac{2}{3}\) hay \(\frac{a+3}{a+6}=\frac{2}{3}\)
\(\Rightarrow\left(a+3\right)3=\left(a+6\right)2\)
\(\Rightarrow3a+9=2a+12\)
\(\Rightarrow a=3\)
Vậy phân số ban đầu là \(\frac{3}{3+11}=\frac{3}{14}\)
Gọi tử số của phân số đó là a \((a\inℤ)\)
Vì tử và mẫu bé hơn là 11
=> mẫu : a + 11
Nếu tăng tử số lên 3 đơn vị và giảm mẫu số đi 5 đơn vị thì được 1 phân số bằng \(\frac{2}{3}\)
Ta có :
\(\frac{a+3}{a+11-5}=\frac{a+3}{a+6}=\frac{2}{3}\)
\(\Rightarrow3(a+3)=2(a+6)\)
\(\Rightarrow3a+9=2a+12\)
\(\Rightarrow a=3\)
Mà : mẫu - tử = 11
=> mẫu số = 14
Vậy phân số ban đầu là : \(\frac{3}{14}\)
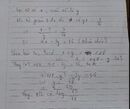
Ta có : 25/13 = 50/26
Nếu ta giữ nguyên tử số là 50 và bớt mẫu số đi 1 đơn vị là : 26 - 1 = 25 thì ta được phân số 50/25 .
50/25 = 2 đúng như yêu cầu của đề bài .
Đ/S :.................................................................................................................................................................................................
nha !
hihihi
hiệu của tử số và mẫu số là
25-13=12
Bớt mẫu số đi một đơn vị ta được phân số có giá trị là 2 => tử số gấp 2 và 1 đơn vị lần mẫu số
từ đó ta có dạng toán là hiệu tỉ bạn tự làm đi nhé