Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc của ô tô chưa tăng là \(v\left(km\text{/}h\right)\)
Theo bài toán, ta có:
\(\dfrac{1}{2}\left(10:v\right)=10:\left(v+10\right)\)
\(\Rightarrow\left(10:v\right):2=10:\left(v+10\right)\)
\(\Leftrightarrow\left(10:v\right):2:2=10:\left(v+10\right):2\)
\(\Leftrightarrow10:v=5:\left(v+10\right)\)
\(\Leftrightarrow10:v:5=5:\left(v+10\right):5\)
\(\Leftrightarrow2:v=v+10\)
\(\Leftrightarrow2:v:2=\left(v+10\right):2\)
\(\Leftrightarrow v=\dfrac{v}{2}+5\)
\(\Leftrightarrow\dfrac{v}{2}-5=0\)
\(\Leftrightarrow v:2=5\)
\(\Rightarrow v=10\)
Vậy vận tốc của ô tô lúc chưa tăng là 10km/h
Gọi vận tốc ban đầu là : \(x\left(km/h\right)-ĐK:x>0\)
Vận tốc sau khi tăng thêm \(10km/h\) là : \(x+10\left(km/h\right)\)
+) Thời gian đi hết quãng đường AB ban đầu : \(\dfrac{10}{x}\left(h\right)\)
+) Thời gian đi hết quãng đường AB nếu tăng vận tốc thêm \(10km/h\) là : \(\dfrac{10}{x+10}\left(h\right)\)
Theo đề bài, ta có pt :
\(2.\dfrac{10}{x+10}=\dfrac{10}{x}\\ < =>\dfrac{2}{x+10}=\dfrac{1}{x}\\ < =>2x=x+10\\ < =>x=10\)
Vậy vận tốc ban đầu : \(10km/h\)

Gọi quãng đường từ Hà Nội đến Đền Hùng là a(km) \(\left(a>0\right)\)
\(\Rightarrow\) thời gian đi là \(\dfrac{a}{30}\) (h)
Theo đề: vận tốc lúc về là \(30+10=40\) (km/h)
\(\Rightarrow\) thời gian về là \(\dfrac{a}{40}\) (h)
36 phút = \(\dfrac{3}{5}\) (h)
Theo đề: \(\dfrac{a}{40}+\dfrac{3}{5}=\dfrac{a}{30}\Rightarrow\dfrac{a+24}{40}=\dfrac{a}{30}\Rightarrow30a+720=40a\)
\(\Rightarrow10a=720\Rightarrow a=72\) (km)
Gọi quãng đường từ Hà Nội đến Đền Hùng là x(km),(x>0).x(km),(x>0).
Vận tốc của ô tô khi đi từ Đền Hùng về Hà Nội là: 30+10=40(km/h)30+10=40(km/h)
Thời gian ô tô đi từ Hà Nội đến Đền Hùng là x30(h).x30(h).
Thời gian ô tô đi từ Đền Hùng về Hà Nội là x40(h).x40(h).
3636 phút =35(h).=35(h).
Vì thời gian về rút ngắn hơn thời gian đi là 3636 phút nên ta có :
x30−x40=35⇔4x120−3x120=72120⇒4x−3x=72⇔x=72(tm)x30−x40=35⇔4x120−3x120=72120⇒4x−3x=72⇔x=72(tm)
Vậy ...

Gọi x (km/h) là vận tốc lúc về. Điều kiện: x > 0
Ta có vận tốc lúc đi là x + 10 (km/h)
Thời gian lúc đi là 150/(x + 10) (giờ)
Thời gian lúc về là 150/x (giờ)
Thời gian nghỉ là 3 giờ 15 phút = 3.(1/4) (giờ) = 13/4 (giờ)
Theo đề bài, ta có phương trình:
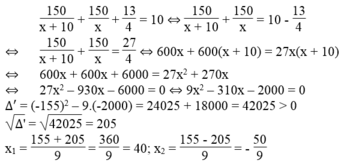
Giá trị x = - 50/9 không thỏa mãn điều kiện bài toán.
Vậy vận tốc ô tô lúc về là 40km/h.

Mọi người giải nhanh giúp mình với, thứ 6 là phải trả bài rối. Gấp lắm ạ!

\(10ph=\dfrac{1}{6}\left(h\right)\)
Gọi vận tốc lúc đi của ô tô là x>0 (km/h)
Thời gian đi: \(\dfrac{50}{x}\left(h\right)\)
Vận tốc lúc về: \(x+10\)
Thời gian về: \(\dfrac{50}{x+10}\)
Ta có pt: \(\dfrac{50}{x}-\dfrac{50}{x+10}=\dfrac{1}{6}\)
\(\Leftrightarrow300\left(x+10\right)-300x=x\left(x+10\right)\)
\(\Leftrightarrow x^2+10x-3000=0\Rightarrow\left[{}\begin{matrix}x=50\\x=-60\left(loại\right)\end{matrix}\right.\)

Gọi quãng đường từ Hà Nội - Thanh Hóa là : x
Thời gian đi nửa quãng đường : \(\frac{x}{2.40}\)
Thời gian đi nữa quảng đường còn lại: \(\frac{x}{2.\left(40+20\right)}\)
Thời gian đi về \(:\frac{x}{50}\)
Tổng thời gian đi là: 9h2p - 2h30p = 6h32 p \(=\frac{98}{15}h\)
Ta có phương trình:
\(\frac{a}{2.40}+\frac{a}{2.\left(40+20\right)}+\frac{a}{50}=\frac{98}{15}\)
\(\Leftrightarrow a=160\)
Vậy quãng đường Hà Nội-Thanh Hóa daì 160km

40 phút = \(\dfrac{2}{3}h.\)
Gọi vận tốc xe dự định đi từ A đến B là x \(\left(km/h\right)\left(x>10\right).\)
thời gian theo dự định là y \(\left(h\right)\left(y>\dfrac{2}{3}\right).\)
\(\Rightarrow\) Quãng đường xe đi được là \(xy\left(km\right).\)
Nếu xe giảm vận tốc đi 10km/h thì xe đến B chậm hơn dự định 1 giờ, nên ta có phương trình:
\(\left(x-10\right)\left(y+1\right)=xy.\left(1\right)\)
Nếu xe tăng vận tốc thêm 10 km/h thì xe đến B sớm hơn dự định 40 phút, nên ta có phương trình:
\(\left(x+10\right)\left(y-\dfrac{2}{3}\right)=xy.\left(2\right)\)
Từ (1) và (2), ta có hpt:
\(\left\{{}\begin{matrix}\left(x-10\right)\left(y+1\right)=xy.\\\left(x+10\right)\left(y-\dfrac{2}{3}\right)=xy.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy+x-10y-10=xy.\\xy-\dfrac{2}{3}x+10y-\dfrac{20}{3}=xy.\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x-10y=10.\\-\dfrac{2}{3}x+10y=\dfrac{20}{3}.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=50.\\y=4.\end{matrix}\right.\left(TM\right)\)
Vậy vận tốc xe dự định đi từ A đến B là 50 km/h.
Gọi vận tốc và thời gian dự định đi từ A đến B lần lượt là v(km/h) và t(h)
(ĐK:v>10,t>\(\dfrac{2}{3}\))
Ta có quãng đường AB dài:vt(km)(1)
_Nếu xe giảm vận tốc đi 10 km thì:
+Vận tốc của xe là:v-10(km/h)
+Thời gian xe đi từ A đến B là:t+1(h)
\(\Rightarrow\)Quãng đường AB dài:(v-10)(t+1)=vt-10t+v-10(km)(2)
_Nếu xe tăng vận tốc thêm 10 km thì:
+Vận tốc của xe là:v+10(km/h)
+Thời gian xe đi từ A đến B là:t-\(\dfrac{2}{3}\)(h)
\(\Rightarrow\)Quãng đường AB dài:(v+10)(t-\(\dfrac{2}{3}\))=vt+10t-\(\dfrac{2}{3}\)v-\(\dfrac{20}{3}\)(km)(3)
Từ (1,2,3) ta có vt-10t+v-10=vt+10t-\(\dfrac{2}{3}\)v-\(\dfrac{20}{3}\)=vt
\(\Leftrightarrow\)\(\begin{cases} v-10t=10 \\ 10t-\dfrac{2}{3}v=\dfrac{20}{3} \end{cases}\)
\(\Leftrightarrow\)\(\begin{cases} v=50 \\ t=4 \end{cases}\)(t/m)
Vậy.........................................................................................
=> thời gian ô tô đến Hà Nội : 200/x (h)
Người lái xe tính rằng nếu tăng vận tốc thêm 10km/h thì về đến Hà Nội sớm nửa giờ
=> 200/x - 200/(x + 10) = 2/3
<=> 400(x + 10) - 400x = x(x + 10)
<=> 400x + 4000 - 400x = x^2 + 10x
<=> x^2 + 10x - 4000 = 0
<=> x = .. .hoặc x =... (loại)
vậy vận tốc của ô tô (nếu không tăng vận tốc) là.......km/h
G