Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

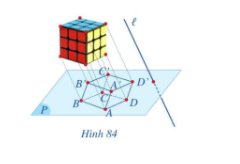
Trường hợp 1: Đặt rubik sao cho các cạnh bên của rubik song song hoặc trùng với đường thẳng ℓ.
Khi đó hình chiếu của rubik trên mp(P) là hình thoi.
Trường hợp 2: Đặt rubik sao cho các cạnh bên của rubik không song song hoặc trùng với đường thẳng ℓ.
Khi đó hình chiếu của rubik trên mp(P) là hình lục giác.
Hình ảnh của khối rubik qua phép chiếu song song lên mặt phẳng (P) theo phương l là hình hộp ABCD.A’B’C’D’

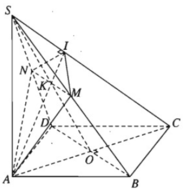
a) Gọi I là giao điểm của mặt phẳng (α) với cạnh SC. Ta có: (α) ⊥ SC, AI ⊂ (α) ⇒ SC ⊥ AI. Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và AI ⊂ (α), nên K là giao điểm của SO với (α).
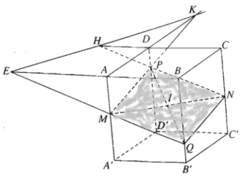
b) Ta có 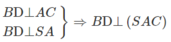
⇒ BD ⊥ SC
Mặt khác BD ⊂ (SBD) nên (SBD) ⊥ (SAC).
Vì BD ⊥ SC và (α) ⊥ SC nhưng BD không chứa trong (α) nên BD // (α)
Ta có K = SO ∩ (α) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của (α) và (SBD).
Mặt phẳng (SBD) chứa BD // (α) nên cắt theo giao tuyến d // BD. Giao tuyến này đi qua K là điểm chung của (α) và (SBD).
Gọi M và N lần lượt là giao điểm của d với SB và SD. Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.

a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB', CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.
Nếu gọi Q là điểm trên cạnh BB' sao cho NQ // PM thì Q là giao điểm của đường thẳng BB' với mặt phẳng (MNP)
Nhận xét. Ta có thể tìm điểm Q bằng cách nối P với trung điểm I của đoạn MN và đường thẳng PI cắt BB' tại Q.
b) Vì mặt phẳng (AA', BB') song song với mặt phẳng (DD', CC') nên ta có MQ // PN. Do đó mặt phẳng (MNP) cắt hình hộp theo thiết diện MNPQ là một ình bình hành.
Giả sử P không phải là trung điểm của đoạn DD'. Gọi H = PN ∩ DC , K = MP ∩ AD. Ta có D = HK là giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
Chú ý rằng giao điểm E = AB ∩ MQ cũng nằm trên giao tuyến d nói trên. Khi P là trung điểm của DD' mặt phẳng (MNP) song song với mặt phẳng (ABCD).

a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB',CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.


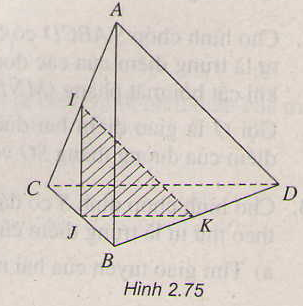
a) Gọi \(N=DK\cap AC;M=DJ\cap BC\).
Ta có \(\left(DJK\right)\cap\left(ABC\right)=MN\Rightarrow MN\subset\left(ABC\right)\)
Vì \(L=\left(ABC\right)\cap JK\) nên dễ thấy \(L=JK\cap MN\)


Câu 1:
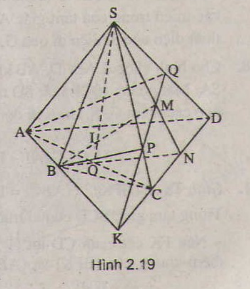
a) Trong (SCD) kéo dài SM cắt CD tại N, Chứng minh N thuộc (SBM)
b) (SBM) ≡ (SBN). Giao tuyến cần tìm là SO
c) Trong (SBN) ta có MB giao SO tại I
d) Trong (ABCD) , ta có AB giao CD tại K, Trong (SCD), ta có KQ giao SC tại P
Từ đó suy ra được giao tuyến của hai mặt phẳng (SCD) và (ABM) là KQ
Câu 2:
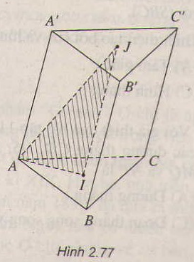
a) Trong (ABCD) gọi M = AE ∩ DC => M ∈ AE, AE ⊂ ( C'AE) => M ∈ ( C'AE). Mà M ∈ CD => M = DC ∩ (C'AE)
b) Chứng minh M ∈ (SDC), trong (SDC) : MC' ∩ SD = F. Chứng minh thiết diện là AEC'F
Câu 3:
a) Chứng minh E, N là hai điểm chung của mặt phẳng (PMN) và (BCD)
b) EN ∩ BC = Q. Chứng minh Q là điểm cần tìm
Câu 4:
a) Chứng minh I, K là hai điểm chung của (BIC) và (AKD)
b) Gọi P = CI ∩ DN và Q = BI ∩ DM, chứng minh PQ là giao tuyến cần tìm
Câu 5:
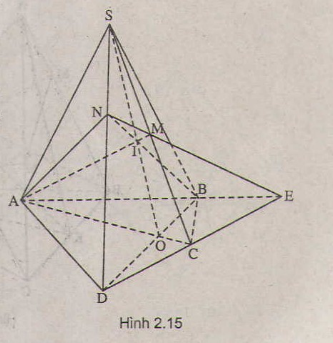
a) Trong mặt phẳng (α) vì AB và CD không song song nên AB ∩ DC = E
=> E ∈ DC, mà DC ⊂ (SDC)
=> E ∈ ( SDC). Trong (SDC) đường thẳng ME cắt SD tại N
=> N ∈ ME mà ME ⊂ (MAB)
=> N ∈ ( MAB). Lại có N ∈ SD => N = SD ∩ (MAB)
b) O là giao điểm của AC và BD => O thộc AC và BD, mà AC ⊂ ( SAC)
=> O ∈( SAC), BD ⊂ (SBD) , O ∈ (SBD)
=> O là một điểm chung của (SAC) và (SBD), mặt khác S cũng là điểm chung của (SAC) và (SBD) => (SAC) ∩ (SBD) = SO
Trong mặt phẳng (AEN) gọi I = AM ∩ BN thì I thuộc AM và I thuộc BN
Mà AM ⊂ (SAC) => I ∈ (SAC), BN ⊂ ( SBD) => I ∈ (SBD). Như vậy I là điểm chung của (SAC) và (SBD) nên I thuộc giao tuyến SO của (SAC) và (SBD) tức là S, I, O thẳng hàng hay SO, AM, BN đồng quy
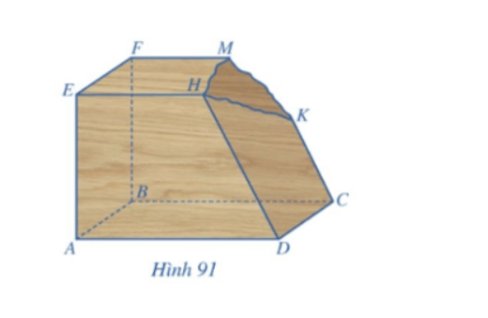


a) Trong mp(CDHK), qua K vẽ đường thẳng song song với CD, cắt DH tại N.
Trong mp(BCKF), qua K vẽ đường thẳng song song với BC, cắt BF tại P.
Ta có: NK // CD, mà CD ⊂ (ACBD) nên NK // (ABCD).
KP // BC, mà BC ⊂ (ACBD) nên KP // (ABCD).
NK, KP cắt nhau tại K trong mp(NPK).
Do đó (NPK) // (ABCD).
Khi đó mp(R) qua K và song song với (ABCD) chính là mp(NPK).
Trong mp(ADHE), qua N vẽ đường thẳng song song với AD, cắt AE tại Q.
Khi đó mp(R) là mp(NKPQ).
Vậy: (NKPQ) ∩ (ADHE) = QN;
(NKPQ) ∩ (CDHK) = NK;
(NKPQ) ∩ (BCKF) = KP;
(NKPQ) ∩ (ABFE) = PQ.
b)Ta có: DH cắt NK tại N, mà NK ⊂ (R) nên giao điểm của DH và (R) là điểm N.
Theo bài, I là giao điểm của DH và (R) nên điểm I và điểm N trùng nhau.
Tương tự ta cũng có điểm J trùng với điểm P.
Ta có: (ABCD) // (EFMH) và (R) // (ABCD) nên (EFMH) // (R) // (ABCD).
Lại có, hai cát tuyến FB, HD cắt ba mặt phẳng song song (EFMH), (R), (ABCD) lần lượt tại F, J, B và H, I, D nên theo định lí Thalès ta có: \(\frac{{FJ}}{{HI}} = \frac{{FB}}{{HD}}\) .
Mặt khác, trong mp(CDKH), tứ giác CDIK có CK // DI (do CK // DH) và IK // CD
Do đó CDIK là hình bình hành, suy ra DI = CK = 40 cm.
Khi đó HI = DH – DI = 75 – 40 = 35 (cm).
Vì vậy, từ \(\frac{{FJ}}{{HI}} = \frac{{FB}}{{HD}}\) ta có: \(\frac{{FJ}}{{35}} = \frac{{60}}{{75}}\) , suy ra \(FJ = \frac{{35.60}}{{75}} = 28\) (cm).
Vậy FJ = 28 cm.