Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thời gian đi hết nửa quãng đường đầu là:
Ta có: \(v_1=\dfrac{s_1}{t_1}\Leftrightarrow t_1=\dfrac{\dfrac{s}{2}}{v_1}=\dfrac{\dfrac{240}{2}}{5}=24\left(s\right)\)
Thời gian đi hết nửa quãng đường sau là:
Ta có: \(v_2=\dfrac{s_2}{t_2}\Leftrightarrow t_2=\dfrac{\dfrac{s}{2}}{v_2}=\dfrac{\dfrac{240}{2}}{6}=20\left(s\right)\)
Thời gian đi hết quãng đường AB là:
\(t_{AB}=t_1+t_2=24+20=44\left(s\right)\)

Câu 1:
Có \(v^2-v_0^2=2aS\Rightarrow S=\frac{v^2-v_0^2}{2a}=\frac{100-25}{4}=18,75\left(m\right)\)
Câu 2:
\(a=-12m/s^2\)=> vật chuyển động chậm dần đều
Câu 3:
Có \(v^2-v_0^2=2aS\Leftrightarrow900-v_A^2=2.2,5.100\Rightarrow v_A=20\left(m/s\right)\)

1.
chọn gốc tọa độ tại A, chiều dương từ A-B, gốc thời gian lúc hai xe xuất phát
x1=x0+v0.t+a.t2.0,5=5t-0,1t2
x2=x0+v0.t+a.t2.0,5=130-1,5t-0,1t2
hai xe gặp nhau x1=x2\(\Rightarrow\)t=20s
quãng đường xe 1, xe 2 đi được đến khi gặp nhau
s1=v0.t+a.t2.0,5=60m
s2=v0.t+a.t2.0,5=70m
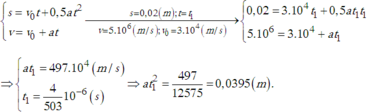


Chọn trục OxOx trùng với đường đi của êlectron. Dùng công thức liên hệ giữa vận tốc, độ dời và gia tốc trong chuyển động thẳng biến đổi đều:
v2−v20=2a(x−x0)=2asv2−v02=2a(x−x0)=2as
Thay số ta có:
(5.106)2−(3.104)2=2a.(2.10−2)(5.106)2−(3.104)2=2a.(2.10−2)
Từ đó suy ra gia tốc a≈6,25.1014m/s2a≈6,25.1014m/s2.
b) Có thể dùng công thức v=v0+atv=v0+at để tính thời gian tt. Ta có:
t=v−v0a=5.106−3.1046,25.1014t=v−v0a=5.106−3.1046,25.1014
t≈8.10−9st≈8.10−9s.
* Chú ý: Ta nhận thấy, tuy gia tốc rất lớn nhưng hạt chỉ nhận gia tốc này trong một thời gian rất nhỏ (cỡ phần tỉ giây). Giá trị này là giá trị điển hình của gia tốc các hạt tích điện trong các máy gia tốc hiện nay.