Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số mét dây thép và cân nặng của dây thép là hai đại lượng tỉ lệ thuận.
Gọi cân nặng của 100m dây thép là x (gam), ( x > 75).
Khi đó áp dụng tính chất của tỉ lệ thuận ta có:
6 75 = 100 x ⇒ x = 100.75 6 = 1250 (gam).
Vậy để bán 100m dây thép thì người bán cần phải cân cho khách hàng 1250 gam dây thép.
Đáp án cần chọn là: D

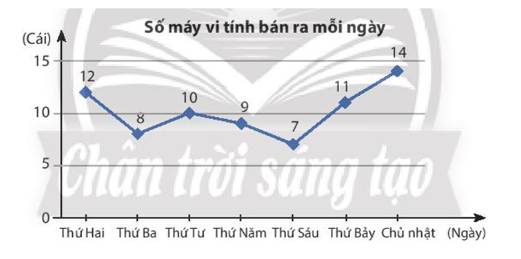
- Biến cố A là biến cố ngẫu nhiên vì cửa hàng có những ngày bán được ít hơn hoặc nhiều hơn 10 máy vi tính
- Biến cố B là biến cố không thể vì cửa hàng luôn bán được ít nhất 7 chiếc máy vi tính trong tất cả các ngày
- Biến cố C là biến cố chắc chắn vì số máy vi tính của cửa hàng bán được nhiều nhất trong 1 ngày là 14 chiếc.

Tóm tắt:
Chiều dài(m) 6 100
Cân nặng(g) 75 x
Giải: Gọi cân nặng của 100m dây thép là x(g) (x>0)
Vì chiều dài và cân nặng là hai đại lượng tỉ lệ thuận nên ta có:
6/75=100/x
x=(75.100):6
x=1250
Vậy để bán 100m dây thép người ta phải can cho khách 1250g

Mọi người giúp mik ik vì ngày mai vào lúc 12h trưa là hạn nộp rr. Ai giúp đc thì giúp mik lun nha.

Gọi số ti vi mỗi loại mà cửa hàng bán được lần lượt là:
\(x;y;z\) (chiếc) \(x;y;z\) \(\in\)N*
Thì số tiền thu được được việc bán mỗi loại ti vi lần lượt là:
20\(x;\) 18\(y\); 15\(z\)
Theo bài ra ta có: 20\(x\) = 18\(y\) = 15\(z\); \(x+y+z=62\)
⇒ \(y\) = \(\dfrac{20}{18}\)\(x\) = \(\dfrac{10}{9}\)\(x\)
z = \(\dfrac{20}{15}\)\(x\) = \(\dfrac{4}{3}x\)
⇒ \(x+\dfrac{10}{9}x+\dfrac{4}{3}x=62\)
\(x\left(1+\dfrac{10}{9}+\dfrac{4}{3}\right)=62\)
\(\dfrac{31}{9}\)\(x\) = 62
\(x\) = 62: \(\dfrac{31}{9}\)
\(x\) = 18
\(y\) = \(\dfrac{10}{9}.18=20\)
\(z=\dfrac{4}{3}.18=24\)
Kết luận: Ti vi sam sung bán được 18 chiếc
Ti vi LG bán được 20 chiếc
Ti vi Xiaomi bán được 24 chiếc
Số thép còn lại sau tuần 1 là: 1,2 x (1 - \(\dfrac{1}{4}\)) = 0,9 (tấn thép)
Số thép còn lại sau tuần 2 là: 0,9 x (1 - \(\dfrac{1}{2}\)) = 0,45 (tấn thép)
Kết luận: Vậy tuần ba họ cần bán 0,45 tấn thép nữa thì hết hàng.