Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Ta có: F k m a x = m g a 0 = 0 , 05 → a 0 = 0 , 1 r a d
+ W t = 1 2 W d ® W = 3 W t = 3 m g l ( 1 - cos a )
+ Áp dụng bảo toàn cơ năng ta được: 3 m g l ( 1 - cos a ) = m g l ( 1 - cos a 0 )
® cos α = 2 + c os α 0 3
+ T = m g ( 3 cos a - 2 cos a 0 ) = 0 , 5025 N
Đáp án B

+ Ta có: Fkmax = mga0 = 0,05 ® a0 = 0,1 rad
+ W t = 1 2 W d → W = 3 Wt = 3mgl(1- cosa)
+ Áp dụng bảo toàn cơ năng ta được: 3mgl(1 - cosa) = mgl(1 - cosa0)
cos α = 2 + cos α 0 3
+ T = mg(3cosa - 2cosa0) = 0,5025 N
ü Đáp án B

D Đáp án B
+ Ta có: Fkmax = mga0 = 0,05 ® a0 = 0,1 rad
+ W t = 1 2 W d => W = 3 Wt = 3mgl(1- cosa)
+ Áp dụng bảo toàn cơ năng ta được: 3mgl(1 - cosa) = mgl(1 - cosa0)
→ cos α = 2 + cos α 0 3
+ T = mg(3cosa - 2cosa0) = 0,5025 N

Đáp án B
Phương pháp: Sử dụng công thức tính lực căng dây của con lắc đơn dao động điều hòa
Cách giải:
+ Biên độ dao động của con lắc: α 0 = 6 0 = π / 30 rad
+ Khi con lắc ở vị trí có
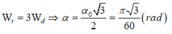
=> Lực căng dây của con lắc:
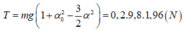
=> Chọn D

Đáp án B
Phương pháp: Sử dụng công thức tính lực căng, thế năng và cơ năng của con lắc đơn
Cách giải:
Trong dao động điều hòa của con lắc đơn thì
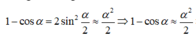
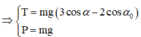
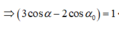

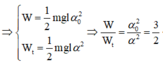
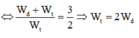

Đáp án B
Phương pháp: Sử dụng công thức tính cơ năng của con lắc đơn dao động điều hoà
W = (1/2)mglα02

Cơ năng của con lắc đơn có chiều dài l, dao động với biên độ góc α 0 là
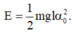
Đáp án C
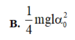
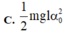
Với con lắc đơn, ta có hệ số hồi phục \(k=\frac{mg}{l}\)
Lực hồi phục: \(F_{hp}=-kx\)
Với x là li độ dài, \(x=\alpha l\)
Suy ra: \(F_{hp}=-\frac{mg}{l}.\alpha l=-mg\alpha\) \(\Rightarrow F_{hpmax}=mg\alpha_0\) \(\Rightarrow\alpha_0=\frac{F_{hpmax}}{mg}=\frac{0,1}{0,1.10}=0,1rad\)(1)
Lực căng dây: \(\tau=mg\left(3\cos\alpha-2\cos\alpha_0\right)=mg\left(3\left(1-2\sin^2\frac{\alpha}{2}\right)-2\left(1-2\sin^2\frac{\alpha_0}{2}\right)\right)=mg\left(1+\alpha_0^2-\frac{3}{2}\alpha^2\right)\)(do góc \(\alpha\) rất nhỏ nên ta lấy gần đúng)
Tại vị trí \(W_t=\frac{1}{2}W_đ\Leftrightarrow W=3W_t\Leftrightarrow\alpha_0^2=3\alpha^2\Leftrightarrow\alpha=\frac{\alpha_0}{\sqrt{3}}\)
Như vậy, lực căng dây tại vị trí này là: \(\tau=mg\left(1+\alpha_0^2-\frac{3}{2}\alpha^2\right)=mg\left(1+\alpha_0^2-\frac{3}{2}\frac{\alpha_0^2}{3}\right)=mg\left(1+\frac{\alpha_0^2}{2}\right)\)
Thay từ (1) vào ta đc: \(\tau=0,1.10\left(1+\frac{0,1^2}{2}\right)=1,005N\)