Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dấu "=" đầu tiên: chỉ là giao hoán vị trí
Dấu "=" thứ hai: sử dụng quy tắc \(cos\left(a+2k\pi\right)=cosa\)
Dấu "=" thứ 3 sử dụng quy tắc: \(cosa=cos\left(-a\right)\)

Dạ 2 đề là 1 ạ tại em muốn ghi lại cho mọi người hiểu ạ

\(\left(x+5\right)\sqrt{2x^2+1}=x^2+x-5\left(đk:x\ge0\right)\)
\(< =>x\sqrt{2x^2+1}-0+5\sqrt{2x^2+1}-5=x\left(x+1\right)\)
\(< =>\frac{x^2\left(2x^2+1\right)}{x\sqrt{2x^2+1}}+\frac{25\left(2x^2+1\right)-25}{5\sqrt{2x^2+1}+5}=x\left(x+1\right)\)
\(< =>\frac{x\left(2x^2+1\right)}{\sqrt{2x^2+1}}+\frac{25.2x^2}{5\left(\sqrt{2x^2+1}+1\right)}-x\left(x+1\right)=0\)
\(< =>x\left[\frac{2x^2+1}{\sqrt{2x^2+1}}+\frac{10x}{\sqrt{2x^2+1}+1}-x-1\right]=0< =>x=0\)
đánh giá cái ngoặc to to bằng đk là được , hoặc có nghiệm nữa thì giải luôn

Đúng đấy mik cũng học lớp ..... nên mik bít . Ủa mà mik học lớp mấy ta ?![]()
![]()
![]()
![]()
![]()

1, \(x^4-19x^2-10x+8=0\)
\(\Leftrightarrow\left(x+4\right)\left(x^3-4x^2-3x+2\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x+1\right)\left(x^2-5x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x+1=0\\x^2-5x+2=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x_1=-4\\x_2=-1\end{matrix}\right.\)
hoặc \(x^2-5x+2=0\)
\(\Rightarrow\Delta=17\left(CT:b^2-4ac\right)\)
\(\Rightarrow\left[{}\begin{matrix}x_3=\dfrac{5+\sqrt{17}}{2}\\x_4=\dfrac{5-\sqrt{17}}{2}\end{matrix}\right.\)
Vậy pt có 4 no là...........

=>2x-2y=1 và 2x+2y=-1
=>4x=0 và x-y=1/2
=>x=0 và y=0-1/2=-1/2
Có cách bấm máy tính 570vn plus không ạ em cần biết cách bấm máy tính ạ

để mk làm nốt cho
\(y^4-2y^3+2y^2-y-2=0\)
<=> \(\left(y^4-2y^3+y^2\right)+\left(y^2-y\right)-2=0\)
<=> \(\left(y^2-y\right)^2+\left(y^2-y\right)-2=0\)
đặt y^2-y=t thì ta có pt \(t^2+t-2=0\)
<= >\(\int_{t=-2}^{t=1}\)
với t=1==> \(y^2-y=1\) từ đó tính ra nghiệm x=\(\frac{1+\sqrt{5}}{2}\) và \(x=\frac{1-\sqrt{5}}{2}\)
với t=-2 thì pt vô nghiệm
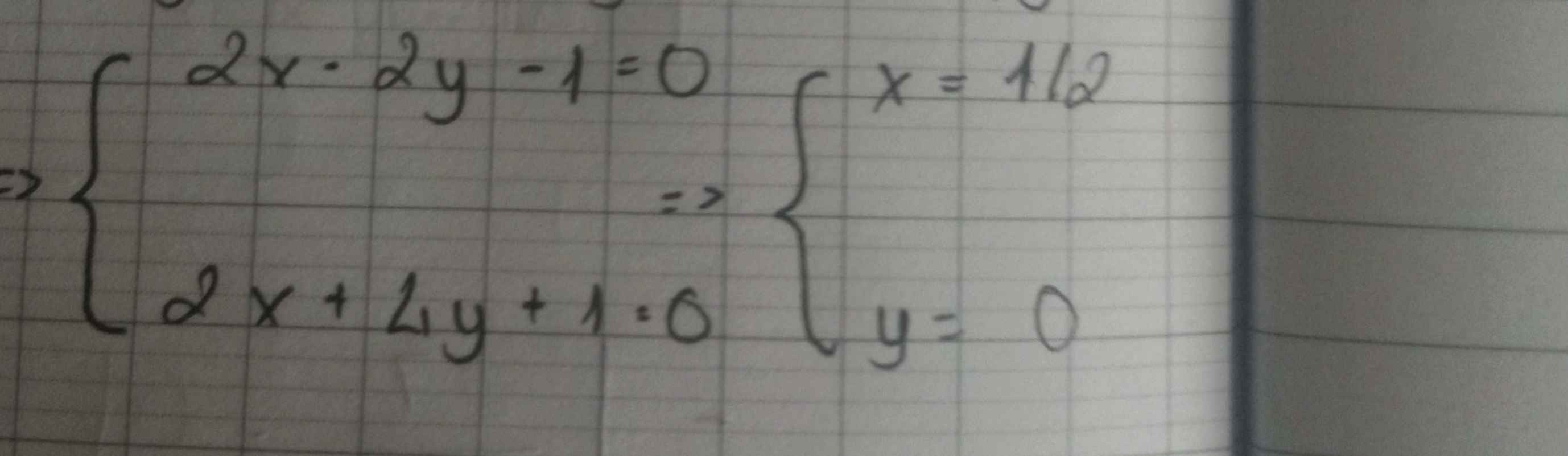
ĐKXĐ: \(\left[{}\begin{matrix}x\ge7\\x\le-2\end{matrix}\right.\)
- Nếu \(2x-1< 0\Leftrightarrow x< \frac{1}{2}\) thì \(\left\{{}\begin{matrix}VT\ge0\\VP< 0\end{matrix}\right.\) BPT hiển nhiên đúng
Kết hợp điều kiện đề bài ta được \(x\le-2\)
- Nếu \(2x-1\ge0\Rightarrow x\ge\frac{1}{2}\) hai vế BPT đều ko âm, bình phương 2 vế:
\(\Leftrightarrow x^2-5x-14\ge4x^2-4x+1\)
\(\Leftrightarrow3x^2+x+15\le0\) (vô nghiệm)
Vậy nghiệm của BPT đã cho là \(x\le-2\)