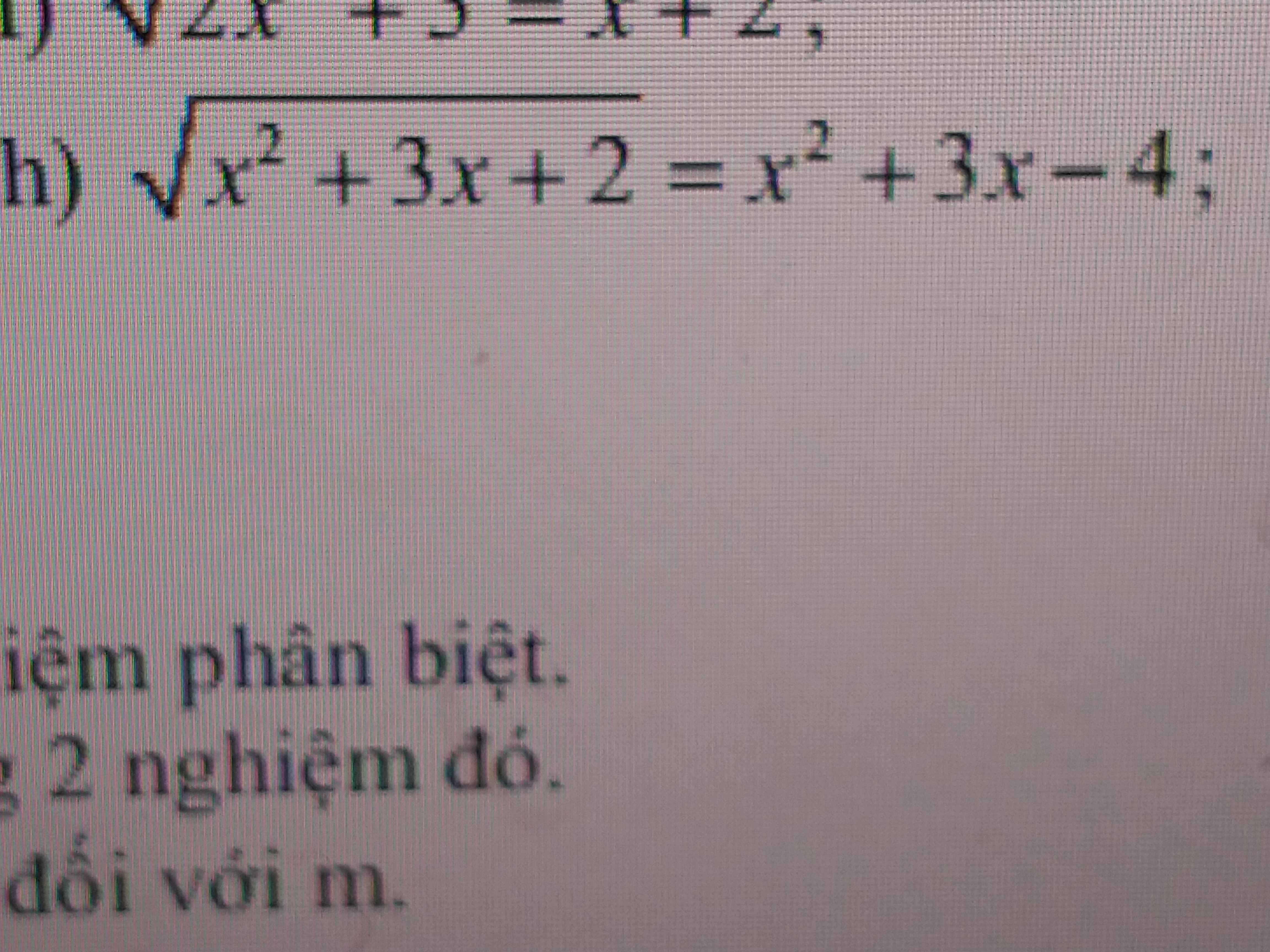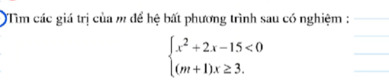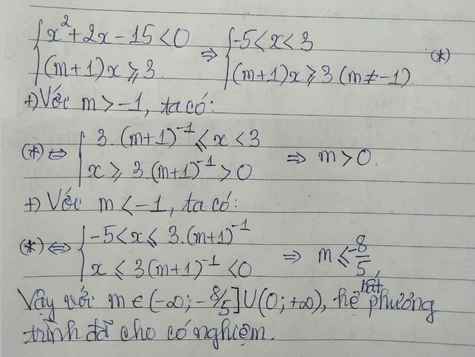K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 11 2021
ĐKXĐ: \(\left[{}\begin{matrix}x\ge-1\\x\le-2\end{matrix}\right.\)
Đặt \(\sqrt{x^2+3x+2}=t\ge0\Rightarrow x^2+3x=t^2-2\)
Pt trở thành:
\(t=t^2-2-4\)
\(\Leftrightarrow t^2-t-6=0\Rightarrow\left[{}\begin{matrix}t=3\\t=-2\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{x^2+3x+2}=3\)
\(\Leftrightarrow x^2+3x+2=9\)
\(\Leftrightarrow x^2+3x-7=0\) (bấm máy)
26 tháng 11 2021
\(PT\Leftrightarrow\sqrt{x^2+3x+2}-3=x^2+3x-7\\ \Leftrightarrow\dfrac{x^2+3x-7}{\sqrt{x^2+3x+2}+3}-\left(x^2+3x-7\right)=0\\ \Leftrightarrow\left(x^2+3x-7\right)\left(\dfrac{1}{\sqrt{x^2+3x+2}+3}-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2+3x-7=0\\\sqrt{x^2+3x+2}+3=1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-3\pm\sqrt{37}}{2}\\\sqrt{x^2+3x+2}=-2\left(\text{vô nghiệm}\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-3+\sqrt{37}}{2}\\x=\dfrac{-3-\sqrt{37}}{2}\end{matrix}\right.\)
Thế vô PT ta thấy 2 nghiệm thỏa mãn
Vậy PT có nghiệm \(S=\left\{\dfrac{-3+\sqrt{37}}{2};\dfrac{-3-\sqrt{37}}{2}\right\}\)
NP
2
NP
2
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2022
\(A\cap B=\varnothing\Leftrightarrow2m-7\le13m+1\)
\(\Leftrightarrow11m\ge-8\Rightarrow m\ge-\dfrac{8}{11}\)
\(\Rightarrow\) Số nguyên m nhỏ nhất là \(m=0\)
NP
2
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 1 2022
Hàm bậc 2 có \(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=6-m\end{matrix}\right.\) nên nghịch biến trên khoảng \(\left(-\infty;6-m\right)\)
Hàm nghịch biến trên khoảng đã cho khi:
\(6-m\ge2\Rightarrow m\le4\)
\(\Rightarrow\) Có 4 giá trị nguyên dương của m
NP
1
NL
1
