K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 12 2022
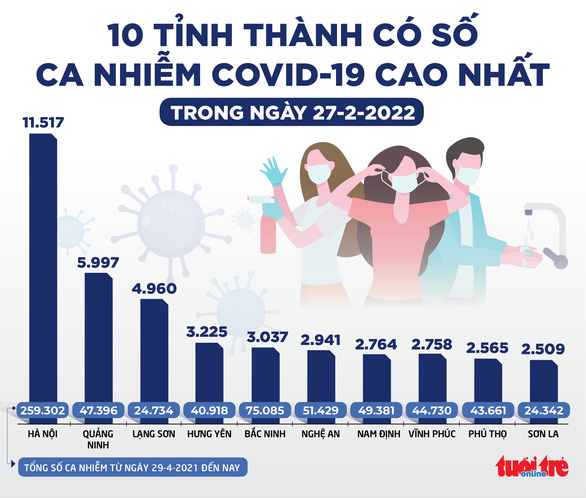
a. Những tỉnh thành phố có ca nhiễm hơn 2800 ca: Nghệ An, Bắc Ninh, Hưng Yên, Lạng Sơn, Quảng Ninh, Hà Nội.
b. Tỉnh có số ca nhiễm Covid 19 cao nhất là: Hà Nội
KV
25 tháng 1 2024
\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)
AH
Akai Haruma
Giáo viên
31 tháng 1 2024
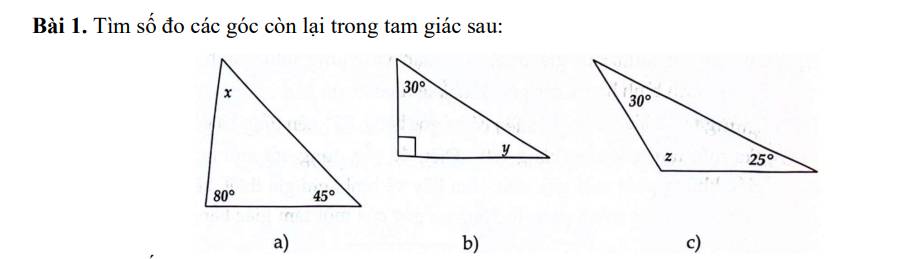
Lời giải:
Áp dụng tính chất tổng 3 góc trong một tam giác bằng $180^0$
a.
$x=180^0-80^0-45^0=55^0$
b.
$y=180^0-30^0-90^0=60^0$
c.
$z=180^0-30^0-25^0=125^0$
KV
4 tháng 12 2023
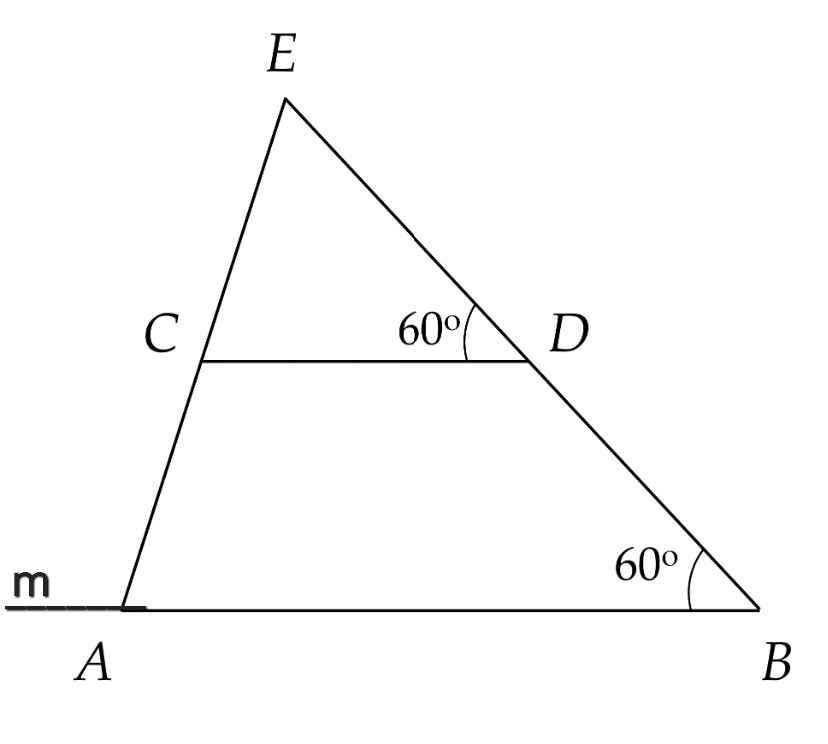
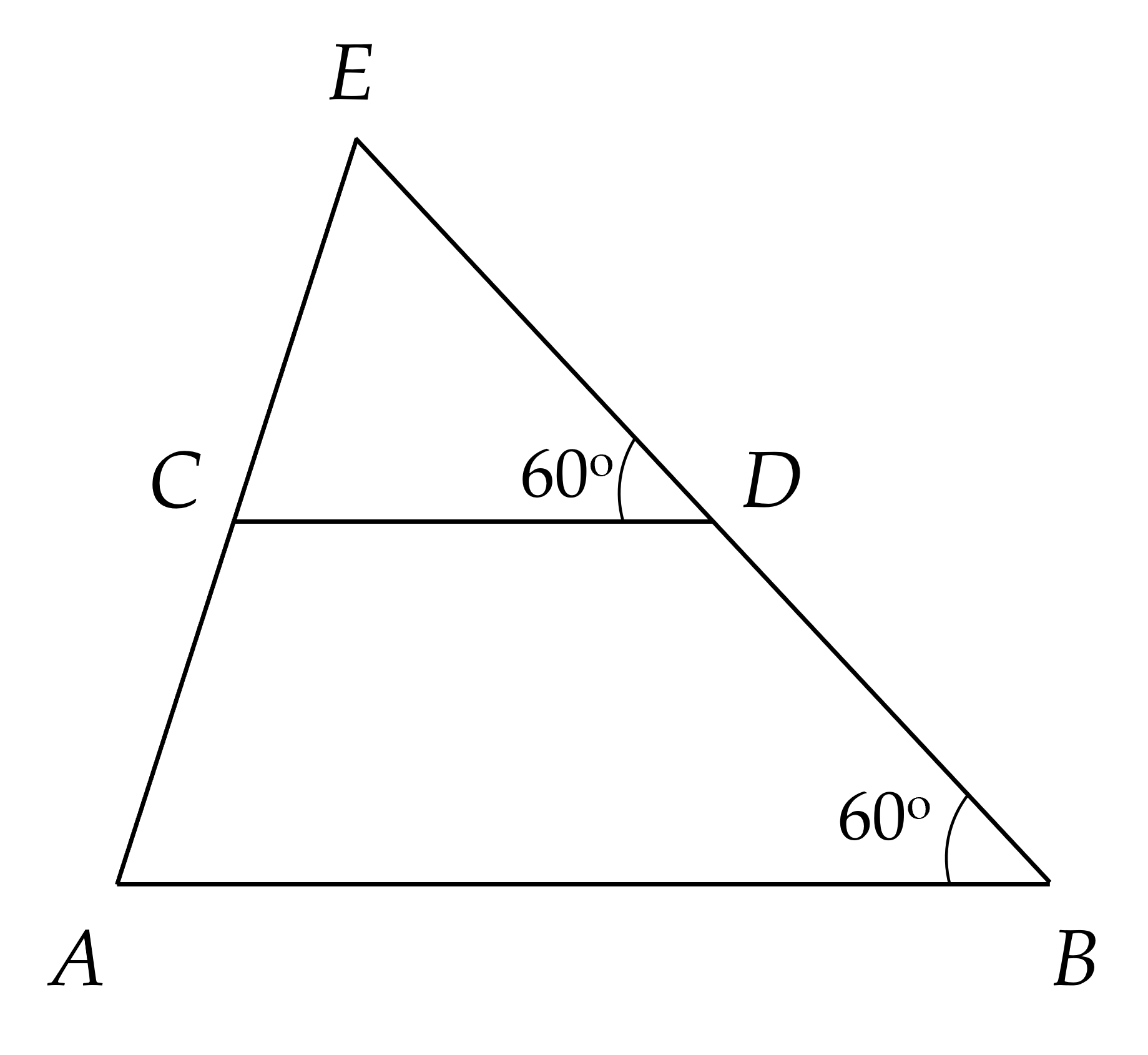
a) Ta có:
∠ABD = ∠CDE = 60⁰ (gt)
Mà ∠ABD và ∠CDE là hai góc so le trong
⇒ AB // CD
b) Vẽ tia Am là tia đối của tia AB
Do AB // CD
⇒ ∠mAC = ∠ACD (so le trong)
Mà ∠mAC + ∠BAC = 180⁰ (kề bù)
⇒ ∠ACD + ∠BAC = 180⁰
TC
6
22 tháng 12 2022
Xét ∆ABC và ∆DBC có:
AB = BD
Góc ABC = góc CBD
Góc BAC = góc BDC
=> ∆ABC = ∆DBC
NT
1
NP
18 tháng 11 2021
bài 5 : Gọi số táo ; cam và nho lần lượt là a ; b ; c ( quả ) ( a , b , c ∈ N* ) và lần lượt tỉ lệ với 4 ; 7 ; 9
Theo bài ra , ta có :
5a - b - c = 16
a\(\dfrac{a}{4}=\dfrac{b}{7}=\dfrac{c}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{a}{4}=\frac{b}{7}=\frac{c}{9}=\frac{5a}{20}=\frac{5a-b-c}{20-7-9}=\frac{16}{4}\)= 4
=> a= 4.4=16
b= 4.7= 28
c=4.9=36
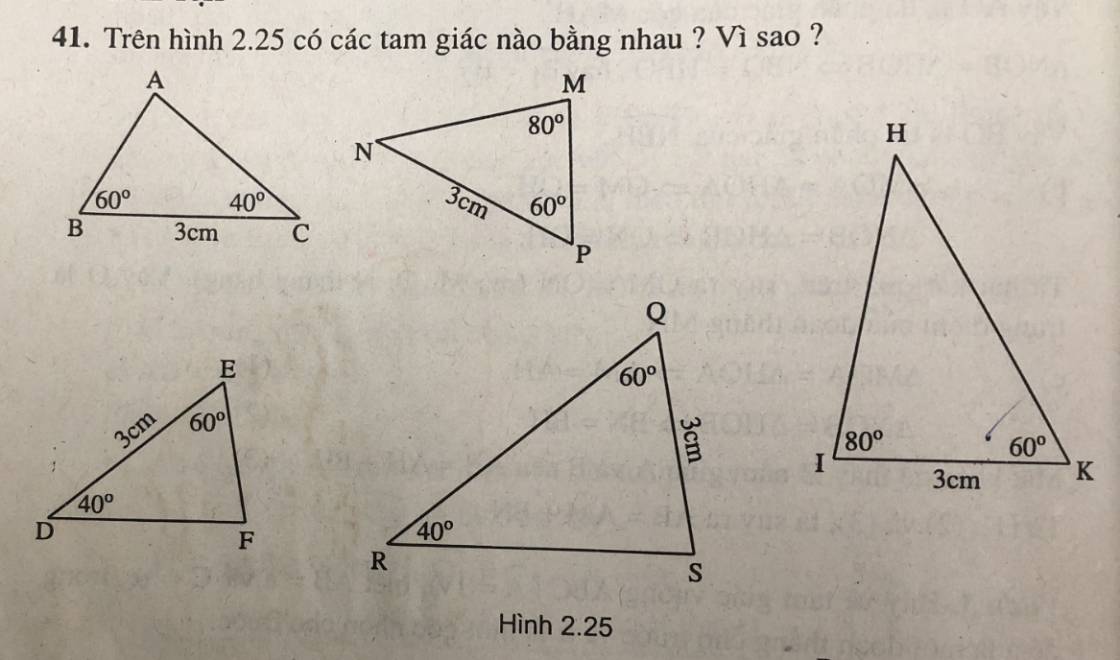
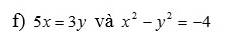
Tính được các góc \(\widehat{BAC}=80^{\circ};\widehat{MNP}=40^{\circ};\widehat{QSR}=80^{\circ};\widehat{IHK}=40^\circ\)
- Vì \(\widehat{B}=\widehat{P};\widehat{C}=\widehat{N};BC=NP\) nên \(\Delta ABC=\Delta MPN\quad\left(g.c.g\right)\)
Tương tự, \(\Delta ABC=\Delta FED\quad\left(g.c.g\right);\Delta MPN=\Delta FED\quad\left(g.c.g\right)\)
- Vì \(\widehat{Q}=\widehat{K};\widehat{S}=\widehat{I};QS=IK\) nên \(\Delta QSR=\Delta KHI\left(g.c.g\right)\)