Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

MÌNH THAM KHẢO NHÉ
a) Xét △ABO và △A′B′O có:
ABOˆ=A′B′Oˆ=900
BOAˆ=B′OA′ˆ (hai góc đối đỉnh)
⇒ Hai tam giác ABO và A'B'O là hai tam giác đồng dạng
⇒ \(\frac{A'B'}{AB}=\frac{B'O}{BO}\)
⇒ Độ phóng đại ảnh \(k=\frac{A'B'}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Tương tự: Hai tam giác A'B'F' và IOF' là hai tam giác đồng dạng
⇒\(\text{ }\frac{B'F'}{OF'}=\frac{A'B'}{IO}=\frac{d'}{d}\)
Áp dụng tính chất của tỉ lệ thức: \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)
⇒\(\frac{1}{f}=\frac{1}{d}=\frac{1}{f'}\)
CÓ MẤY CÁI KÍ HIỆU GÓC, MÌNH KHÔNG BIẾT VIẾT, BẠN THÔNG CẢM
a) Xét \(\Delta ABO\) và \(\Delta A'B'O'\)
\(ABO=A'B'O=90^0\)
\(BOA=B'O'A\)( hai góc đối đỉnh )
\(\Rightarrow\)Hai tam giác ABO và A'B'O là hai tam giác đồng dạng
\(\Rightarrow\frac{A'B}{AB}=\frac{B'O}{BO}\)
\(\Rightarrow\)Độ phóng đại ảnh : \(k=\frac{A'B}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Tương tự : Hai tam giác A'B'F và IOF' là hai tam giác đồng dạng
\(\Rightarrow\frac{B'F'}{OF}=\frac{A'B}{TO}=\frac{d'}{d}\)
Dựa vào tính chất của tỉ lệ thức : \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)

a) Dựng ảnh
O A B A' B' F I
b)
Xét các tam giác đồng dạng
IOF với A'B'F \(\Rightarrow \dfrac{IO}{A'B'}=\dfrac{OF}{B'F}\)
ABO với A'B'O \(\Rightarrow \dfrac{IO}{A'B'}=\dfrac{BO}{B'O}\)
Lại có: \(IO=AB\)
Từ đó bạn biến đổi tiếp nhé.

Từ hình vẽ, vì A ≡ F và tia tới BI song song với trục chính nên hình ABIO là hình chữ nhật có AI và BO là hai đường chéo cắt nhau tại trung điểm của mỗi đường → B’ là trung điểm của BO
Mà A’B’ // AB nên A’B’ là đường trung bình của tam giác ABO
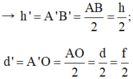

Trên hình 42-43.5a, xét hai cặp tam giác đồng dạng:
ΔABO và ΔA’B’O; ΔA’B’F’ và ΔOIF’.
Từ hệ thức đồng dạng được: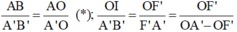
Vì AB = OI (tứ giác BIOA là hình chữ nhật)
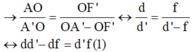
Chia cả hai vế của (1) cho tích d.d’.f ta được:
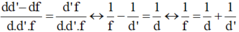
(đây được gọi là công thức thấu kính cho trường hợp ảnh thật)
Thay d = 2f, ta tính được: OA’ = d’ = 2f = d
Thay vào (*) ta được: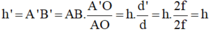
Vậy d’ = d; h’ = h.

Nếu còn tiếp tục cop bài thiếu Tham Khảo từ hoidap247 nữa sẽ trực tiếp báo cáo lên admin box Lí khoá acc !!!

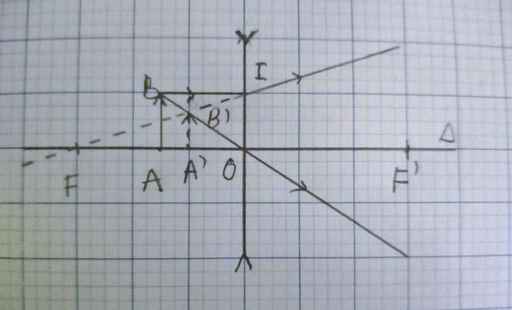
Tham khảo hình vẽ!!!
\(\Delta OAB\sim\Delta OA'B'\)
\(\Rightarrow\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}\Rightarrow\dfrac{4}{A'B'}=\dfrac{4}{OA'}\left(1\right)\)
\(\Delta FA'B'\sim\Delta FOI\)
\(\Rightarrow\dfrac{OI}{A'B'}=\dfrac{OF}{OF-OA'}=\dfrac{OA}{A'B'}\)
\(\Rightarrow\dfrac{4}{A'B'}=\dfrac{12}{12-OA'}\left(2\right)\)
\(\Rightarrow\dfrac{4}{OA'}=\dfrac{12}{12-OA'}\Rightarrow OA'=3cm\)
\(\Rightarrow A'B'=\dfrac{AB\cdot OA'}{OA}=\dfrac{4\cdot3}{4}=3cm\)
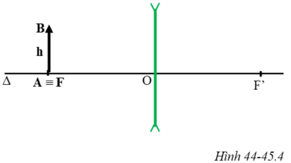
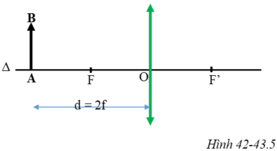
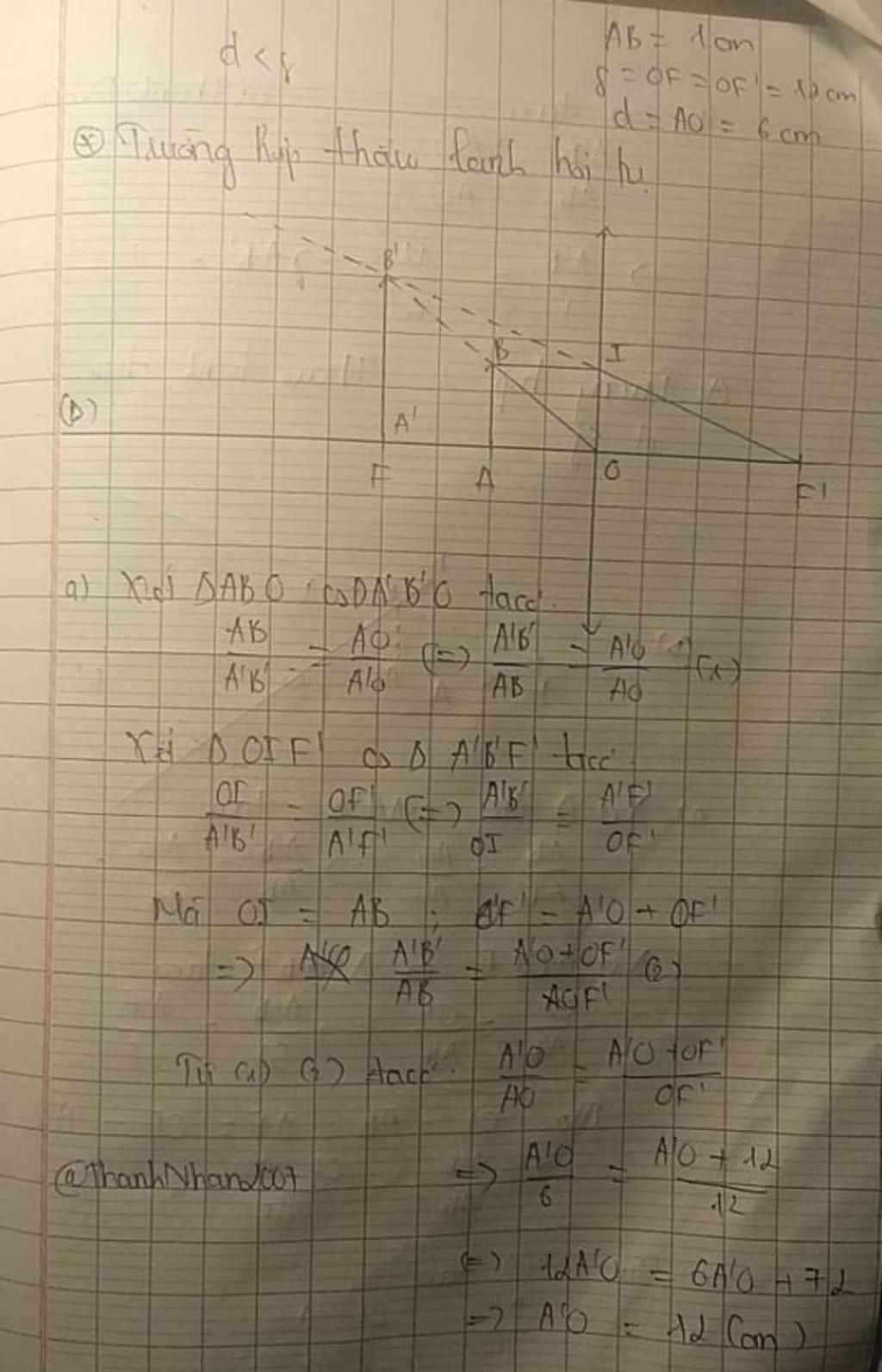
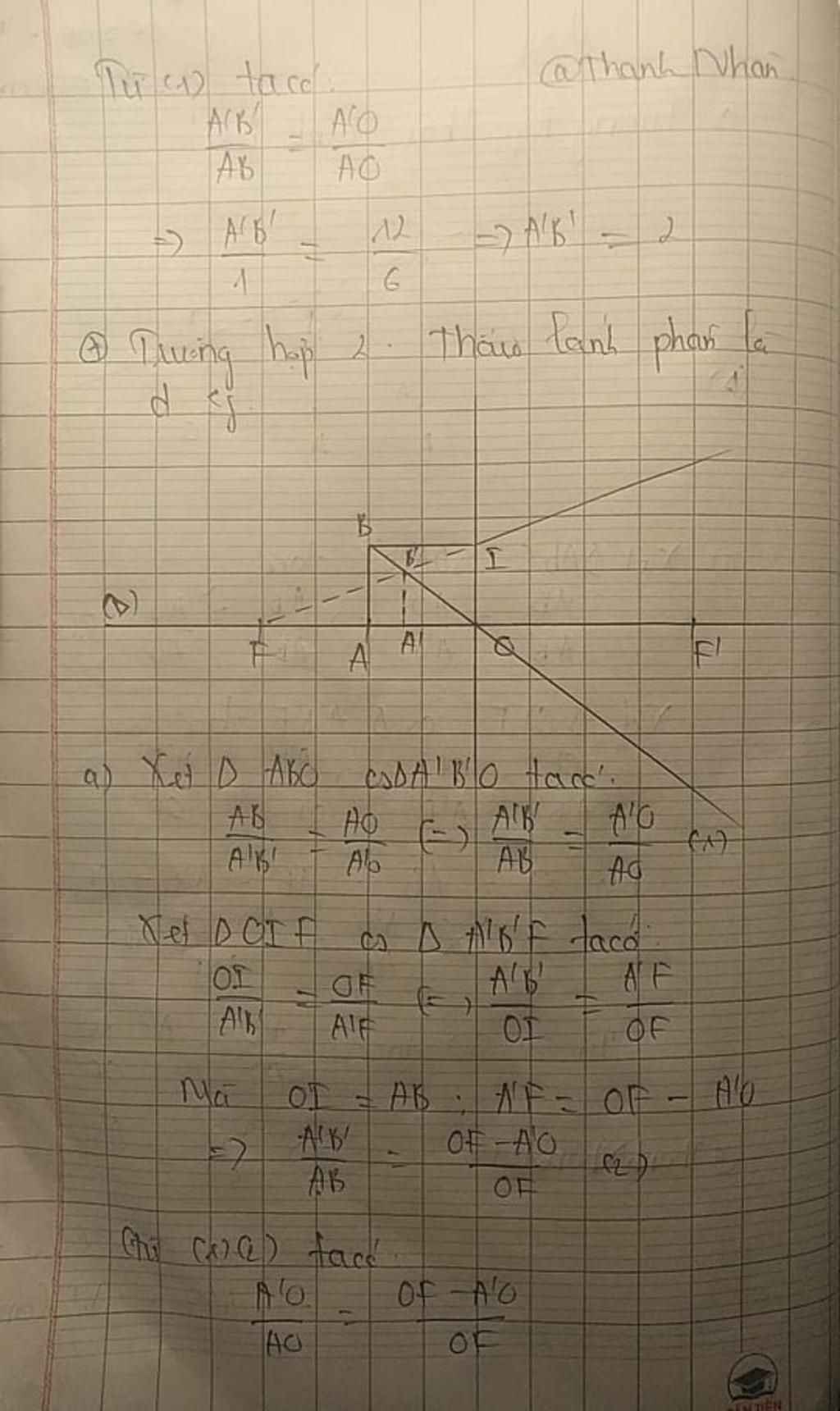

bạn tự vẽ hình nha !!!!
\(\Delta\) A'B'O \(\sim\) \(\Delta\)ABO(g.g)
\(\Rightarrow\)\(\frac{A'B'}{AB}=\frac{A'O}{AO}\Rightarrow\frac{h'}{h}=\frac{d'}{d}\)