Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


d/
\(\Leftrightarrow\frac{2}{\sqrt{29}}sinx-\frac{5}{\sqrt{29}}cosx=\frac{5}{\sqrt{29}}\)
Đặt \(cosa=\frac{2}{\sqrt{29}}\) với \(0< a< \pi\)
\(\Rightarrow sinx.cosa-cosx.sina=sina\)
\(\Leftrightarrow sin\left(x-a\right)=sina\)
\(\Rightarrow\left[{}\begin{matrix}x-a=a+k2\pi\\x-a=\pi-a+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2a+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
c/
\(\Leftrightarrow\frac{\sqrt{3}}{\sqrt{19}}cosx+\frac{4}{\sqrt{19}}sinx=\frac{\sqrt{3}}{\sqrt{19}}\)
Đặt \(cosa=\frac{\sqrt{3}}{\sqrt{19}}\) với \(0< a< \pi\)
\(\Rightarrow cosx.cosa+sinx.sina=cosa\)
\(\Leftrightarrow cos\left(x-a\right)=cosa\)
\(\Rightarrow\left[{}\begin{matrix}x-a=a+k2\pi\\x-a=-a+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2a+k2\pi\\x=k2\pi\end{matrix}\right.\)

a) cosx – √3sinx = √2 ⇔ cosx – tan π/3sinx = √2 ⇔ cos π/3cosx – sinπ/3sinx = √2cosπ/3 ⇔ cos(x +π/3) = √2/2 ⇔ b) 3sin3x – 4cos3x = 5 ⇔ 3/5sin3x – 4/5cos3x = 1. Đặt α = arccos thì phương trình trở thành cosαsin3x – sinαcos3x = 1 ⇔ sin(3x – α) = 1 ⇔ 3x – α = π/2 + k2π ⇔ x = π/6 +α/3 +k(2π/3) , k ∈ Z (trong đó α = arccos3/5). c) Ta có sinx + cosx = √2cos(x – π/4) nên phương trình tương đương với 2√2cos(x – π/4) – √2 = 0 ⇔ cos(x – π/4) = 1/2 ⇔ d) 5cos2x + 12sin2x -13 = 0 ⇔ Đặt α = arccos5/13 thì phương trình trở thành cosαcos2x + sinαsin2x = 1 ⇔ cos(2x – α) = 1 ⇔ x = α/2 + kπ, k ∈ Z (trong đó α = arccos 5/13).

a.
\(\Leftrightarrow sin2x+cos2x=3sinx+cosx+2\)
\(\Leftrightarrow2sinx.cosx-3sinx+2cos^2x-cosx-3=0=0\)
\(\Leftrightarrow sinx\left(2cosx-3\right)+\left(cosx+1\right)\left(2cosx-3\right)=0\)
\(\Leftrightarrow\left(sinx+cosx+1\right)\left(2cosx-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=-1\\2cosx-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}\\cosx=\frac{3}{2}\left(vn\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\frac{\pi}{4}=-\frac{\pi}{4}+k2\pi\\x+\frac{\pi}{4}=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
b.
\(\Leftrightarrow1+sinx+cosx+2sinx.cosx+2cos^2x-1=0\)
\(\Leftrightarrow sinx\left(2cosx+1\right)+cosx\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(2cosx+1\right)=0\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\frac{\pi}{4}\right)\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\frac{\pi}{4}\right)=0\\cosx=-\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{4}+k\pi\\x=\frac{2\pi}{3}+k2\pi\\x=-\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)

ĐKXĐ: ...
Chia 2 vế cho \(cosx\) ta được:
\(\frac{1}{cos^2x}=3tanx+5\)
\(\Leftrightarrow1+tan^2x=3tanx+5\)
\(\Leftrightarrow tan^2x-3tanx-4=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{4}+k\pi\\x=arctan\left(4\right)+k\pi\end{matrix}\right.\)
Có 4 nghiệm thỏa mãn: \(x=\left\{-\frac{\pi}{4};\frac{3\pi}{4};arctan\left(4\right)-\pi;arctan\left(4\right)\right\}\)

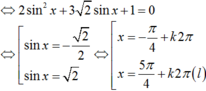
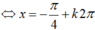
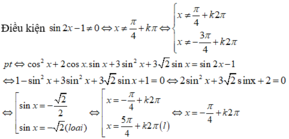
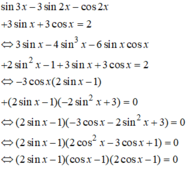
A. \(a^2+b^2-c^2=3+1-4=0\) thỏa mãn
B. \(a^2+b^2-c^2=9+25-36=-2< 0\)
Phương trình vô nghiệm
Và rồi đáp án B đúng à?