Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x\left(x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
\(x\sqrt{x}\left(x-1\right)^2=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
B là đáp án đúng

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

Chọn B
TH1.Nếu a-1=0 hay a =1 thì
(1) thành: 2 > 0 ( luôn đúng mọi x) Tập nghiệm của bất phương trình T = R
(2) thành: 2x+1> 0 hay x> -1/2 Tập nghiệm của bất phương trình 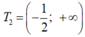
Vậy a= 1 không thỏa yêu cầu bài toán.
TH2. Nếu a+1= 0 hay a= -1thì
(1) thành: -2x=4>0 hay x< 2. Tập nghiệm của bất phương trình T2 = (-∞; 2)
(2) thành: 3> 0 luôn đúng Tập nghiệm của bất phương trình T= R
Vậy a= -1 không thỏa yêu cầu bài toán.
TH3. 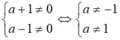
(1) : (a-1) x> a-3 và (2) : (a+1) x> a-2
Hai bất phương trình tương đương
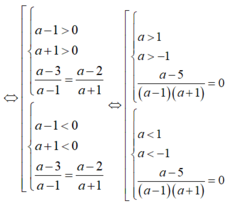
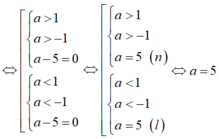

c) x^2 -x-20=0
⇔x2−5x+4x−20=0⇔x2−5x+4x−20=0
⇔(x2+4x)−(5x+20)=0⇔(x2+4x)−(5x+20)=0
⇔x(x+4)−5(x+4)=0⇔x(x+4)−5(x+4)=0
⇔(x+4)(x−5)=0⇔(x+4)(x−5)=0
⇔[x+4=0x−5=0⇔[x=−4x=5⇔[x+4=0x−5=0⇔[x=−4x=5
Vậy...

a: Thay x=-1 và y=2 vào 2x-y+3, ta được:
\(2x-y+3=-2-2+3=-1< 0\)
=>(-1;2) không là nghiệm của bất phương trình 2x-y+3>0
b:
-x+2+2(y-2)<2(2-x)(1)
=>-x+2+2y-4<4-2x
=>-x+2y-2-4+2x<0
=>x+2y-6<0
Thay x=-1 và y=2 vào x+2y-6, ta được:
\(x+2y-6=-1+4-6=-3< 0\)
=>(-1;2) là nghiệm của bất phương trình (1)
c: Thay x=-1 và y=2 vào x-y-15, ta được:
\(x-y-15=-1-2-15=-18< 0\)
=>(-1;2) là nghiệm của bất phương trình x-y-15<0
d: 3(x-1)+4(y-2)<5x-3(2)
=>3x-3+4y-8<5x-3
=>3x+4y-11-5x+3<0
=>-2x+4y-8<0
=>x-2y+4>0
Khi x=-1 và y=2 thì \(x-2y+4=-1-4+4=-1< 0\)
=>(-1;2) không là nghiệm của bất phương trình (2)

Thử trực tiếp ta thấy ngay x = -3 là nghiệm của bất phương trình (1) nhưng không là nghiệm bất phương trình (2), vì vậy (1) và (2) không tương đương do đó phép bình phương hai vế một bất phương trình không phải là phép biến đổi tương đương.

Đáp án A: \(x + y > 3\) là bất phương trình bậc nhất hai ẩn x và y có a=1, b=1, c=3
Đáp án B: \({x^2} + {y^2} \le 4\) không là bất phương trình bậc nhất hai ẩn vì có \({x^2},{y^2}\)
Đáp án C: \(\left( {x - y} \right)\left( {3x + y} \right) \ge 1 \Leftrightarrow 3{x^2} - 2xy - {y^2} \ge 1\) không là bất phương trình bậc nhất hai ẩn vì có \({x^2},{y^2}\)
Đáp án D: \({y^3} - 2 \le 0\) không là bất phương trình bậc nhất hai ẩn vì có \({y^3}\).
Chọn A

a) \(2{x^2} + 3x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 2{x^2} + 3x + 1\) có 2 nghiệm phân biệt \(x = - 1,x = \frac{{ - 1}}{2}\)
hệ số \(a = 2 > 0\)
Ta có bảng xét dấu f(x) như sau:
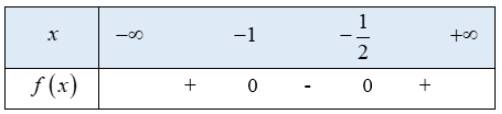
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 1\\x \ge - \frac{1}{2}\end{array} \right.\)
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)\)
b) \( - 3{x^2} + x + 1 > 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + x + 1\) có 2 nghiệm phân biệt \(x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}\)
Hệ số \(a = - 3 < 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) > 0\)\( \Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}\)
Vậy tập nghiệm của bất phương trình là \(\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)\)
c) \(4{x^2} + 4x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 4{x^2} + 4x + 1\) có nghiệm duy nhất \(x = \frac{{ - 1}}{2}\)
hệ số \(a = 4 > 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\)
d) \( - 16{x^2} + 8x - 1 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 16{x^2} + 8x - 1\) có nghiệm duy nhất \(x = \frac{1}{4}\)
hệ số \(a = - 16 < 0\)
Ta có bảng xét dấu f(x) như sau:
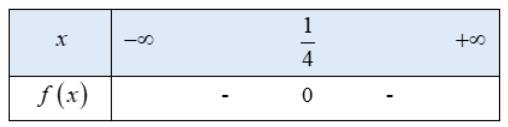
Từ bảng xét dấu ta thấy \(f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}\)
e) \(2{x^2} + x + 3 < 0\)
Ta có \(\Delta = {1^2} - 4.2.3 = - 23 < 0\) và có \(a = 2 > 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} + x + 3\) mang dấu “-” là \(\emptyset \)
Vậy tập nghiệm của bất phương trình \(2{x^2} + x + 3 < 0\) là \(\emptyset \)
g) \( - 3{x^2} + 4x - 5 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + 4x - 5\) có \(\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) = - 11 < 0\) và có \(a = - 3 < 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - 3{x^2} + 4x - 5\) mang dấu “-” là \(\mathbb{R}\)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 4x - 5 < 0\) là \(\mathbb{R}\)
Ta có: x 2 − 3 x = 0 ⇔ x = 0 x = 3
Do đó, tập nghiệm của phương trình đã cho là S 0 = 0 ; 3 .
Xét các đáp án:
- Đáp án A. Ta có: x 2 + x − 2 = 3 x + x − 2
⇔ x − 2 ≥ 0 x 2 − 3 x = 0 ⇔ x ≥ 2 x = 0 x = 3 ⇔ x = 3
Do đó, tập nghiệm của phương trình là S 1 = 3 ≠ S 0
- Đáp án B. Ta có: x 2 + 1 x − 3 = 3 x + 1 x − 3 ⇔ x − 3 ≠ 0 x 2 − 3 x = 0 ⇔ x = 0
Do đó, tập nghiệm của phương trình là S 2 = 0 ≠ S 0 .
- Đáp án C. Ta có
x 2 x − 3 = 3 x x − 3 ⇔ x − 3 ≥ 0 x 2 − 3 x = 0 x − 3 = 0 ⇔ x ≥ 3 x = 0 x = 3 ⇔ x = 3
Do đó, tập nghiệm của phương trình là S 3 = 3 ≠ S 0 .
- Đáp án D. Ta có: x 2 + x 2 + 1 = 3 x + x 2 + 1 ⇔ x 2 = 3 x ⇔ x = 0 x = 3
Do đó, tập nghiệm của phương trình là S 4 = 0 ; 3 ≠ S 0 .
Đáp án cần chọn là: D