Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
a) Vẽ đường thẳng \(\Delta : - 2x + y - 1 = 0\) đi qua hai điểm \(A(0;1)\) và \(B\left( { - 1; - 1} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 2.0 + 0 - 1 = - 1 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)

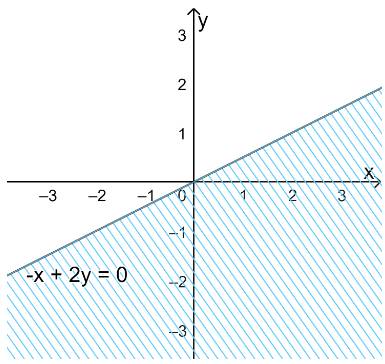
b) Vẽ đường thẳng \(\Delta : - x + 2y = 0\) đi qua hai điểm \(O(0;0)\) và \(B\left( {2;1} \right)\)
Xét điểm \(A(1;0).\) Ta thấy \(A \notin \Delta \) và \( - 1 + 2.0 = - 1 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), không chứa điểm A (1;0)
(miền không gạch chéo trên hình)
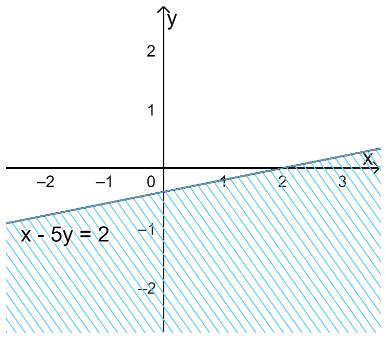
c) Vẽ đường thẳng \(\Delta :x - 5y = 2\) đi qua hai điểm \(A(2;0)\) và \(B\left( { - 3; - 1} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 - 5.0 = 0 < 2\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
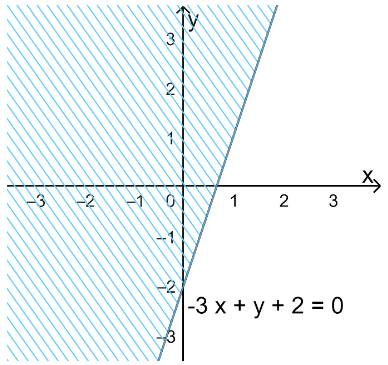
d) Vẽ đường thẳng \(\Delta : - 3x + y + 2 = 0\) đi qua hai điểm \(A(0; - 2)\) và \(B\left( {1;1} \right)\)
Xét điểm \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 3.0 + 0 + 2 = 2 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), không chứa điểm O (0;0)
(miền không gạch chéo trên hình)
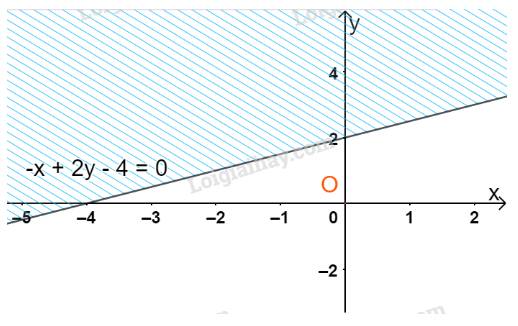
e) Ta có: \(3(x - 1) + 4(y - 2) < 5x - 3 \Leftrightarrow - 2x + 4y - 8 < 0 \Leftrightarrow - x + 2y - 4 < 0\)
Vẽ đường thẳng \(\Delta : - x + 2y -4 = 0\) đi qua hai điểm \(A(0;2)\) và \(B\left( {-4;0} \right)\)
Xét điểm \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 0 + 2.0 -4 = -4 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa điểm O (0;0)
(miền không gạch chéo trên hình)

Đáp án D là đáp án đúng
Thế tọa độ O lần lượt vào các đáp án thì A: \(2\le0\) (sai), B: \(2\le0\) (sai), C:\(-2\ge0\) (sai)
D: \(2\ge0\) (đúng)

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

Đáp án A: \(x + y > 3\) là bất phương trình bậc nhất hai ẩn x và y có a=1, b=1, c=3
Đáp án B: \({x^2} + {y^2} \le 4\) không là bất phương trình bậc nhất hai ẩn vì có \({x^2},{y^2}\)
Đáp án C: \(\left( {x - y} \right)\left( {3x + y} \right) \ge 1 \Leftrightarrow 3{x^2} - 2xy - {y^2} \ge 1\) không là bất phương trình bậc nhất hai ẩn vì có \({x^2},{y^2}\)
Đáp án D: \({y^3} - 2 \le 0\) không là bất phương trình bậc nhất hai ẩn vì có \({y^3}\).
Chọn A

Thay các cặp số vào bất phương trình đã cho ta thấy chỉ có cặp số (4;4) thỏa mãn bất phương trình. Đáp án là D.

Bất phương trình bậc nhất 2 ẩn :
\(2x+3y>0\Rightarrow Câu\) \(C\)
\(x-2y\le1\Rightarrow Câu\) \(f\)
\(4\left(x-1\right)+5\left(y-3\right)>2x-9\)
\(\Leftrightarrow4x-4+5y-15-2x+9>0\)
\(\Leftrightarrow2x+5y-10>0\) \(\Rightarrow Câu\) \(i\)

Hàm số ở câu a) \(y = 9{x^2} + 5x + 4\) là hàm số bậc hai với \(a = 9,b = 5,c = 4\)
Hàm số ở câu b), c) không phải là hàm số bậc hai vì chứa \({x^3}\)
Hàm số ở câu d) \(y = 5{x^2} + \sqrt x + 2\) không phải là hàm số bậc hai vì chứa \(\sqrt x \)
a: Thay x=-1 và y=2 vào 2x-y+3, ta được:
\(2x-y+3=-2-2+3=-1< 0\)
=>(-1;2) không là nghiệm của bất phương trình 2x-y+3>0
b:
-x+2+2(y-2)<2(2-x)(1)
=>-x+2+2y-4<4-2x
=>-x+2y-2-4+2x<0
=>x+2y-6<0
Thay x=-1 và y=2 vào x+2y-6, ta được:
\(x+2y-6=-1+4-6=-3< 0\)
=>(-1;2) là nghiệm của bất phương trình (1)
c: Thay x=-1 và y=2 vào x-y-15, ta được:
\(x-y-15=-1-2-15=-18< 0\)
=>(-1;2) là nghiệm của bất phương trình x-y-15<0
d: 3(x-1)+4(y-2)<5x-3(2)
=>3x-3+4y-8<5x-3
=>3x+4y-11-5x+3<0
=>-2x+4y-8<0
=>x-2y+4>0
Khi x=-1 và y=2 thì \(x-2y+4=-1-4+4=-1< 0\)
=>(-1;2) không là nghiệm của bất phương trình (2)