Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B

Gọi A là một điểm thuộc d => tọa độ của A thỏa mãn HPT


Đáp án B
Phương trình mặt phẳng (Q) có dạng: x - 2y - 3z + m = 0 (m ≠ 10).
Vì (Q) đi qua điểm A(2; -1; 0) nên ta có 2 + 2 + m = 0 <=> m = -4.
Vậy phương trình mặt phẳng (Q) là x - 2y - 3z -4 = 0 hay -x + 2y + 3z + 4 = 0.

Mặt phẳng ( β ) song song với trục Oy và vuông góc với mặt phẳng ( α ):
2x – y + 3z + 4 = 0, do đó hai vecto có giá song song hoặc nằm trên ( β ) là: j → = (0; 1; 0) và n α → = (2; −1; 3)
Suy ra ( β ) có vecto pháp tuyến là n β → = j → ∧ n α → = (3; 0; −2)
Mặt phẳng ( β ) đi qua điểm M(2; -1; 2) có vecto pháp tuyến là: n β → = (3; 0; −2)
Vậy phương trình của ( β ) là: 3(x – 2) – 2(z – 2) = 0 hay 3x – 2z – 2 = 0

Ta có: M(x, y, z) ∈ (P)
⇔ d(M, ( P 1 )) = d(M, ( P 2 ))
⇔|2x + y + 2z + 1| = |2x + y + 2z + 5|
⇔ 2x + y + 2z + 1 = – (2x + y + 2z + 5)
⇔ 2x + y + 2z + 3 = 0
Từ đó suy ra phương trình của (P) là: 2x + y + 2z + 3 = 0.

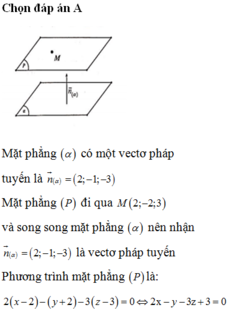
Đáp án A
Vì mặt phẳng (P) song song với mặt phẳng (Q): 2x – y + 2z = 0 nên mặt phẳng (P) có dạng: 2x – y + 2z + d = 0
Mà mặt phẳng (P) đi qua điểm A(2; -1; -2) nên:
2.2 –(-1) + 2.(-2) + d = 0 nên d = -1
Vậy phương trình mặt phẳng (P) là: 2x – y + 2z – 1= 0

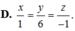
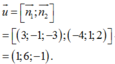
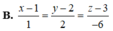

Chọn \(M\left(-5;0;3\right)\) là điểm nằm trên giao tuyến của (P) và (Q)
\(\overrightarrow{n_P}=\left(1;-3;2\right)\) ; \(\overrightarrow{n_Q}=\left(2;1;-3\right)\)
\(\Rightarrow7\overrightarrow{u}=\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=7\left(1;1;1\right)\)
Trục Ox có 1 vtcp là \(\overrightarrow{u_1}=\left(1;0;0\right)\)
\(\left[\overrightarrow{u};\overrightarrow{u_1}\right]=\left(0;1;-1\right)\)
Phương trình mặt phẳng cần tìm có dạng:
\(y-1\left(z-3\right)=0\Leftrightarrow y-z+3=0\)