K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 8 2021
Có \(sin^23x\le1;sin^2x\le1;sin3x\ge-1\)
\(\Rightarrow\left\{{}\begin{matrix}4sin^23x.sin^2x\le4\\6+2sin3x\ge6+2.-1=4\end{matrix}\right.\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}sin^23x=1\\sin^2x=1\\sin3x=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}sin3x=1\\cos^2x=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)\(\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
Vậy...
HP
24 tháng 8 2021
1.
\(sin^3x+cos^3x\le sin^2x+cos^2x=1\)
\(2-sin^4x\ge1\Leftrightarrow sin^4x\le1\)
\(\Rightarrow sin^3x+cos^3x\le2-sin^4x\)
Đẳng thức xảy ra khi:
\(\left\{{}\begin{matrix}sin^3x+cos^3x=1\\sin^4x=1\end{matrix}\right.\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
HP
24 tháng 8 2021
2.
\(\left(sinx+\sqrt{3}cosx\right)sin3x=2\)
\(\Leftrightarrow\left(\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx\right)sin3x=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)sin3x=1\)
\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{3}\right)-cos\left(4x+\dfrac{\pi}{3}\right)=2\)
Ta có:
\(cos\left(4x+\dfrac{\pi}{3}\right)\ge-1\Rightarrow-cos\left(4x+\dfrac{\pi}{3}\right)\le1\)
\(cos\left(2x-\dfrac{\pi}{3}\right)\le1\)
\(\Rightarrow cos\left(2x-\dfrac{\pi}{3}\right)-cos\left(4x+\dfrac{\pi}{3}\right)\le1-\left(-1\right)=2\)
Đẳng thức xảy ra khi:
\(\left\{{}\begin{matrix}cos\left(2x-\dfrac{\pi}{3}\right)=1\\cos\left(4x+\dfrac{\pi}{3}\right)=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-\dfrac{\pi}{3}=k2\pi\\4x+\dfrac{\pi}{3}=\pi+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
Tìm 2 giá trị của x để hàm \(f\left(x\right)\) nhận kết quả trái dấu là được.
a.
Đặt \(f\left(x\right)=\left(1-m^2\right)x^3-6x-1\)
Hàm \(f\left(x\right)\) là hàm đa thức nên liên tục trên R
\(f\left(0\right)=-1< 0\) (chọn \(x=0\) do nó làm triệt tiêu tham số m, thường sẽ ưu tiên chọn những giá trị x kiểu thế này. Ở câu này, có đúng 1 giá trị x khiến m triệt tiêu nên phải chọn thêm)
\(f\left(-1\right)=m^2-1+6-1=m^2+4>0\) với mọi m (để ý rằng ta đã có \(f\left(0\right)\) âm nên cần chọn x sao cho \(f\left(x\right)\) dương, mà \(-m^2\) nên ta nên chọn x sao cho nó chuyển dấu thành \(m^2\))
\(\Rightarrow f\left(0\right).f\left(-1\right)< 0;\forall m\)
\(\Rightarrow\) Hàm luôn có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\) với mọi m
Hay với mọi m thì pt luôn luôn có nghiệm
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
b.
Đặt \(f\left(x\right)=\left(m^2+m+5\right)\left(3-x\right)^{2021}x+x-4\)
\(f\left(x\right)\) là hàm đa thức nên liên tục trên R
\(f\left(0\right)=-4< 0\)
(Tới đây, nếu ta chọn tiếp \(x=3\) để triệt tiêu m thì cho \(f\left(3\right)=-1\) vẫn âm, ko giải quyết được vấn đề, nên ta phải chọn 1 giá trị khác. Thường trong những trường hợp xuất hiện \(m^2\) thế này, cố gắng chọn x sao cho hệ số của \(m^2\) dương (nếu cần \(f\left(x\right)\) dương, còn cần \(f\left(x\right)\) âm thì chọn x sao cho hệ số \(m^2\) âm). Ở đây dễ nhất là chọn \(x=2\) , vì khi đó \(\left(3-2\right)^{2021}=1\) vừa đảm bảo hệ số \(m^2\) dương vừa dễ tính toán, nếu chọn \(x=1\) cũng được thôi nhưng quá to sẽ rất khó biến đổi)
\(f\left(2\right)=\left(m^2+m+5\right).\left(3-2\right)^{2021}.2+2-4=2\left(m^2+m+5\right)-2\)
\(=2m^2+2m+8=2\left(m+\dfrac{1}{2}\right)^2+\dfrac{15}{2}>0;\forall m\)
\(\Rightarrow f\left(0\right).f\left(2\right)< 0;\forall m\Rightarrow\) hàm luôn có ít nhất 1 nghiệm thuộc \(\left(0;2\right)\) với mọi m
Hay pt đã cho luôn có nghiệm với mọi m
TG
0
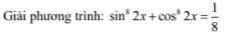
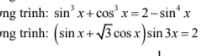
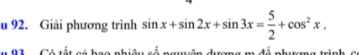
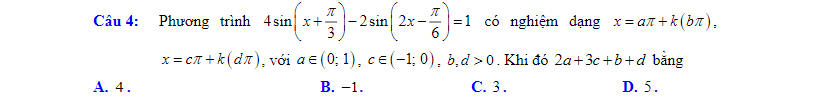
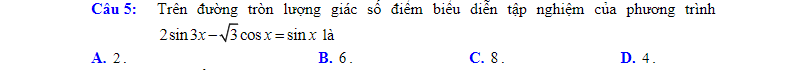
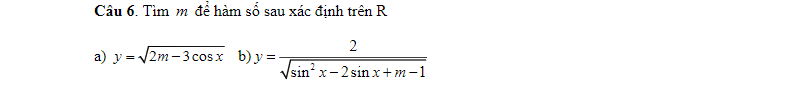
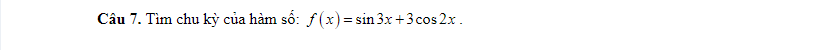
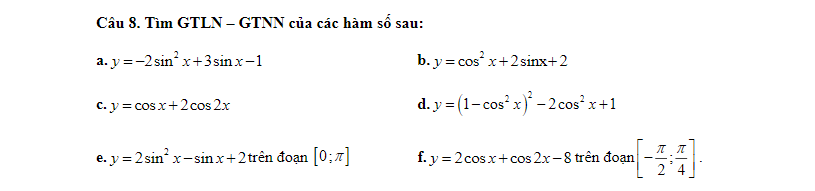
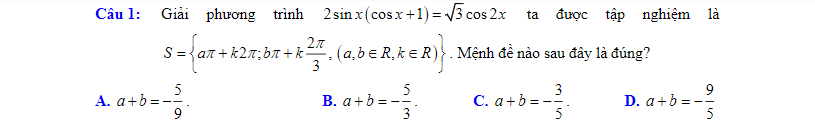
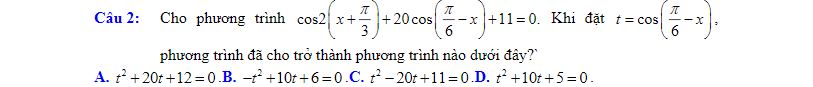
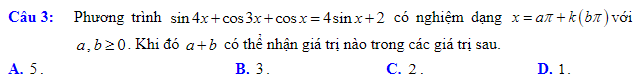
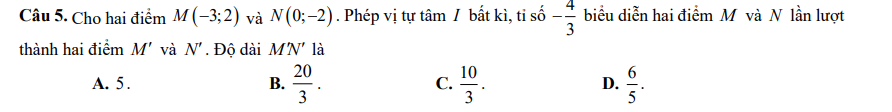
Áp dụng BĐT bunhiacopxki có:
\(\left(sin^42x+cos^42x\right)\left(1+1\right)\ge\left(sin^22x+cos^22x\right)^2\)\(\Rightarrow sin^42x+cos^42x\ge\dfrac{1}{2}\)
\(\left(sin^82x+cos^82x\right)\left(1+1\right)\ge\left(sin^42x+cos^42x\right)^2\ge\dfrac{1}{4}\)\(\Rightarrow sin^82x+cos^82x\ge\dfrac{1}{8}\)
Dấu "=" xảy ra khi \(sin^22x=cos^22x=\dfrac{1}{2}\)\(\Rightarrow sin^22x.cos^22x=\dfrac{1}{4}\)
\(\Leftrightarrow sin^24x=1\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{8}+\dfrac{k\pi}{2}\\x=-\dfrac{\pi}{8}+\dfrac{k\pi}{2}\end{matrix}\right.\)
Vậy...