Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ADBK có
M là trung điểm chung của AB và DK
=>ADBK là hình bình hành
=>AK=DB
mà DB=AC(ABCD là hình chữ nhật)
nên AK=AC
=>ΔAKC cân tại A
b: Xét ΔIAM có IE là phân giác
nên \(\dfrac{ME}{EA}=\dfrac{IM}{IA}\)
mà IA=IK
nên \(\dfrac{ME}{EA}=\dfrac{IM}{IK}\)
Xét ΔIMK có IF là phân giác
nên \(\dfrac{IM}{IK}=\dfrac{MF}{FK}\)
=>\(\dfrac{ME}{EA}=\dfrac{MF}{FK}\)
Xét ΔMAK có \(\dfrac{ME}{EA}=\dfrac{MF}{FK}\)
nên EF//AK
Ta có: EF//AK
AK//BD(AKBD là hình bình hành)
Do đó: EF//BD

a.
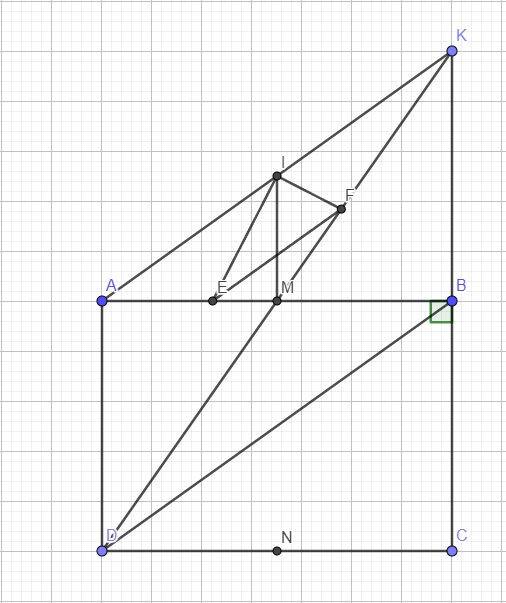
Xét tứ giác ADBK có: hai đường chéo AB và DK cắt nhau tại trung điểm M của mỗi đường
\(\Rightarrow ADBK\) là hình bình hành
Do ABCD là hình chữ nhật \(\Rightarrow AB\perp BC\Rightarrow AB\) là đường cao tam giác ACK
Theo cmt, ADBK là hbh \(\Rightarrow BK=AD\)
Mà \(AD=BC\) (ABCD là hcn)
\(\Rightarrow BK=BC\Rightarrow AB\) là trung tuyến tam giác ACK
\(\Rightarrow AB\) vừa là đường cao vừa là trung tuyến nên tam giác ACK cân tại A
b.
Do IE là phân giác, áp dụng định lý phân giác trong tam giác IAM:
\(\dfrac{EM}{EA}=\dfrac{IM}{IA}\) (1)
Do IF là phân giác, áp dụng định lý phân giác trong tam giác IMK:
\(\dfrac{FM}{FK}=\dfrac{IM}{IK}\) (2)
Mà I là trung điểm AK \(\Rightarrow IA=IK\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{EM}{EA}=\dfrac{FM}{FK}\Rightarrow EF||AK\) (định lý Talet đảo)
Theo c/m câu a do ADBK là hình bình hành \(\Rightarrow AK||BD\)
\(\Rightarrow EF||BD\)

B M C N A D P Q H E F
a, Ta có: \(\widehat{MAN}=\widehat{DBC}=45^0\Rightarrow AQMB\) nội tiếp. \(\left(1\right)\)
b, Từ \(\left(1\right)\Rightarrow\widehat{MQA}+\widehat{MBA}=180^0\Rightarrow\widehat{AQM}=90^0\left(\widehat{ABC}=90^0\right)\)
\(\Rightarrow MQ\perp AN\)
Tương tự như trên ta có: \(NP\perp AM\Rightarrow H\) là trực tâm của \(\Delta AMN\)
\(\Rightarrow AH\perp MN\left(đpcm\right)\)
c, Gọi \(AH\)\(∩\) \(MN=E\)
Gọi \(AF\perp AM,F\in CD\Rightarrow\widehat{FAD}=\widehat{BAM}\left(+\widehat{MAD}=90^0\right)\)
Lại có: \(\widehat{ADF}=\widehat{ABM}=90^0,AD=AB\Rightarrow\Delta ADF=\Delta ABM\left(g-c-g\right)\)
\(\Rightarrow AF=AM\)
Lại có: \(\widehat{NAF}=\widehat{MAN}=45^0\Rightarrow\Delta FAN=\Delta MAN\left(c-g-c\right)\)
\(\Rightarrow MN=FN\Rightarrow MN+NC+CM=NF+NC+CM=DN+CN+DF+CM\)
\(=\left(DN+CN\right)+\left(BM+CM\right)=CD+CB=2AD\)
Lại có tiếp: \(\hept{\begin{cases}AE\perp MN\\AD\perp NF\end{cases}}\Rightarrow AE=AD\)
\(\Rightarrow S_{ANM}=\frac{1}{2}.AE.MN=\frac{1}{2}.AD.MN\)
Lại có tiếp: \(MN\le MC+NC\)
\(\Rightarrow2MN\le MN+MC+NC=2AD\)
\(\Rightarrow MN\le AD\)
\(\Rightarrow S_{ANM}=\frac{1}{2}.AD.MN\le\frac{1}{2}AD^2\)
Dấu " = " xảy ra \(\Leftrightarrow\orbr{\begin{cases}M\equiv B\\M\equiv C\end{cases}}\)
(Rối thực sự -.- )

tự vẽ hình nha
lấy Q trung điểm CD
kẻ AQ =>AQ song song CM
cm AQ vuông góc DN {tự cm}
tam giác DCI có AQ song song CM nên \(\frac{DQ}{QC}=\frac{DE}{EI}\) với E là giao điểm ND và AQ
tam giác ĐẠI có ĐỀ là đường cao và trung tuyến nên là tam giác vuông
tick nha

Bước 1: Chứng minh tam giác BEF vuông
Vì F là trung điểm AD, ta có AF = FD. Và do tam giác vuông ADE có E nằm trên đường chéo, ta có AE = 3EC. Vậy, tổng các tỉ số các cạnh của tam giác vuông ADE là: AE/EC = AF/FD = 3.
Theo định lý đường phân giác trong tam giác, đường phân giác của một góc trong tam giác chia đôi cạnh đối diện với góc đó theo tỉ lệ của các cạnh. Vì vậy, BE chia FD thành hai phần bằng nhau.
Vì BF là đường phân giác của góc ABD trong tam giác ABE và chia đôi cạnh đối diện (FD), nên BF cũng chia BE thành hai phần bằng nhau.
Do đó, ta có BF = FE.
Bước 2: Chứng minh tam giác BEF cân
Ta đã chứng minh được BF = FE . Và ta đã biết BE = EF vì F là trung điểm của AD. Do đó, ta có BF = FE = BE.
Vậy tam giác BEF là tam giác vuông cân
Đề bài phải sửa thành AN=NC mới c/m được
A B C D
MA=MB (gt)
AN=NC (gt)
=> MN là đường trung bình của tg ABC
=> MN//BC và \(MN=\dfrac{BC}{2}\)
Ta có
\(BC\perp AB\) mà MN//BC => \(MN\perp AB\) (1)
Ta có
\(BC=AB\Rightarrow MN=\dfrac{AB}{2}\)
Mà \(MA=MB=\dfrac{AB}{2}\)
=> MN = MA (2)
Từ (1) và (2) => tg AMN vuông cân tại M