Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

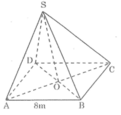
Đáy ABCD là hình vuông nên △ OAB vuông cân tại O.
Áp dụng định lí pi-ta-go ta tính được OA bằng 32
Ta có: SO ⊥ OA nên tam giác AOA cân tại O.
Áp dụng Pi-ta-go vào tam giác vuông SOA ta tỉnh được SO bằng 32
Vậy chọn đáp án C.

Tham khảo:
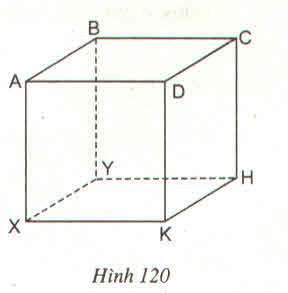
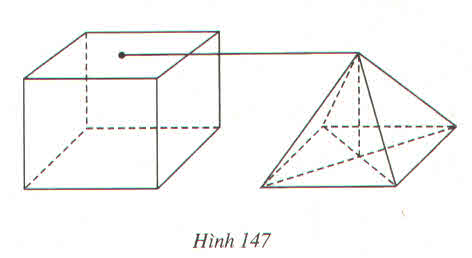
a. Những cặp mặt phẳng song song với nhau là:
mp (ABCD) và mp (XYHK)
mp (ADKX) và mp (BCHY)
mp (ABYX) và mp (CDKH)
b. Những cặp mặt phẳng vuông góc với nhau là:
mp (ABCD) và mp (ADKX); mp (XYHK) và mp (ADKX)
mp (ABCD) và mp (ABYX); mp (XYHK) và mp (ABYX)
mp (ABCD) và mp (BCHY); mp (XYHK) và mp (BCHY)
mp (ABCD) và mp (CDKH); mp (XYHK) và mp (CDKH)
mp (ADKX) và mp (CDKH); mp (ADKX) và mp (ABYX)
mp (BCHY) và mp (CDKH); mp (BCHY) và mp (ABYX)
c. Hai mặt phẳng (BCHY) và (KXYH) vuông góc với nhau.
d: 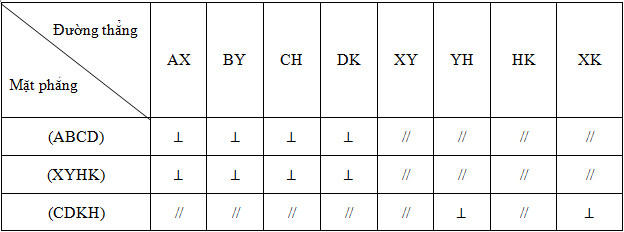

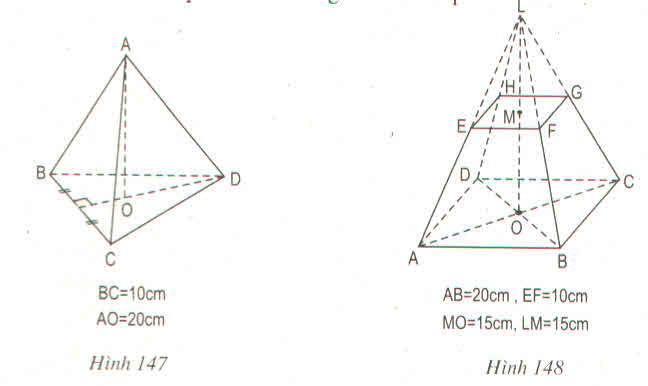
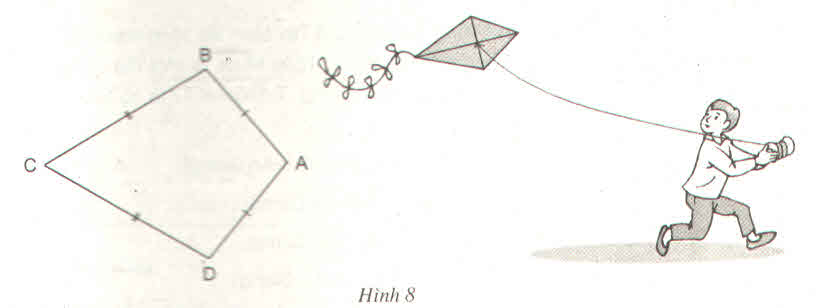
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)

Suy ra: ⇒ \(\widehat{B}=\widehat{D}\)
Ta có \(\widehat{B}+\widehat{D}=360^o-\left(100^o+60^o\right)=200^o\)
Do đó \(\widehat{B}=\widehat{D}=100^o\)
Bài giải:
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)

Suy ra: ⇒ˆB=ˆD⇒B^=D^
Ta có ˆB+ˆD=3600−(100+60)=200B^+D^=3600−(100+60)=200
Do đó ˆB=ˆD=1000B^=D^=1000

a)
∆ABC có MN // BC.
=> MNCBMNCB = AKAHAKAH(kết quả bài tập 10)
Mà AK = KI = IH
Nên AKAHAKAH = 1313 => MNCBMNCB = 1313 => MN = 1313BC = 1313.15 = 5 cm.
∆ABC có EF // BC => EFBCEFBC = AIAHAIAH = 2323
=> EF = 2323.15 =10 cm.
b) Áp dụng kết quả ở câu b của bài 10 ta có:
SAMN= 1919.SABC= 30 cm2
SAEF= 4949.SABC= 120 cm2
Do đó SMNEF = SAEF - SAMN = 90 cm2
bt 10 là bt nào?
vs lại toàn Áp Dụng bài người khác, ko cm?!

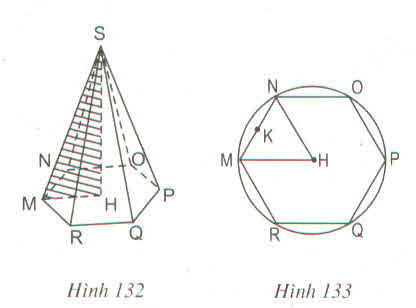
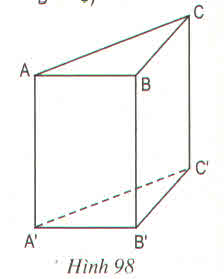
a) Những cặp mặt phẳng song song nhau: (ABC) // (A'B'C')
b) Những cặp mặt phẳng vuông góc với nhau: (ABB'A') ⊥ (A'B'C); (ACC'A') ⊥ (A'B'C'); (BCC'B') ⊥ (A'B'C); (ABB'A') ⊥ (ABC); (ACC'A') ⊥ (ABC); (BCC'B') ⊥ (ABC)
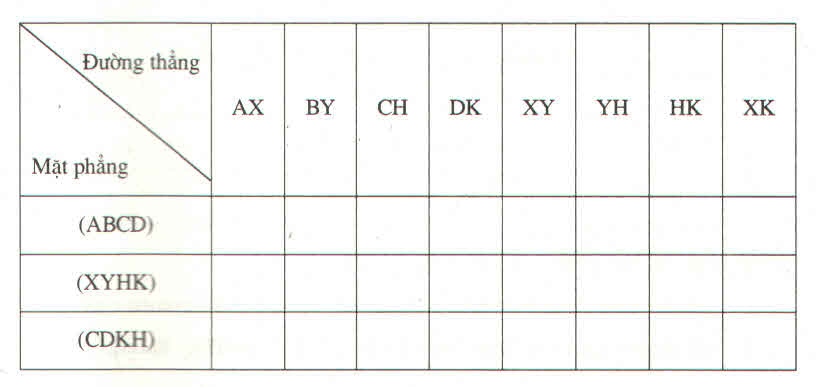
c) Điền vào ô trống:

a) Đáy của hình lăng trụ đứng là một tam giác vuông cân
b) Các mặt bên nhận được không phải tất cả là hình vuông
\(\Bigg(\) hai hình vuông và một hình chữ nhật \(\Bigg)\)








(C) \(\sqrt{32}\)m