Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

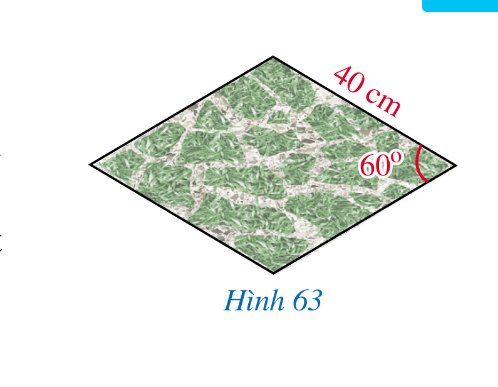
Giả sử viên gạch dạng hình thoi là hình thoi ABCD có.
AB = 40 cm; O là giao điểm của AC và BD
Xét \(\Delta DAB\) có: AB = AD = 40 cm; \( \Rightarrow \Delta DAB\) là tam giác đều suy ra
BD = AB = AD = 40cm \( \Rightarrow OB = \dfrac{{BD}}{2} = \dfrac{{40}}{2} = 20cm\)
Xét \(\Delta AOB\) vuông tại O có: \(O{A^2} + O{B^2} = A{B^2} \Rightarrow O{A^2} = A{B^2} - O{B^2} = {40^2} - {20^2} = 1200\)
\( \Rightarrow OA = \sqrt {1200} \Rightarrow AC = 2\sqrt {1200} \)
Diện tích của hình thoi ABCD là: \(S = \dfrac{1}{2}.AC.BD = \dfrac{1}{2}.40.2\sqrt {1200} = 1385,64(c{m^2})\)
Vậy diện tích của viên gạch đó là: \(1385,64(c{m^2})\)

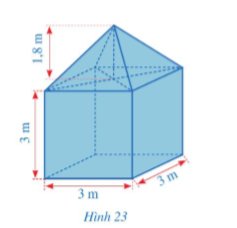
Thể tích của lều trại đó là.
\(V = {3^3} + \dfrac{1}{3}{3^2}.1,8 = 32,4({m^3})\)

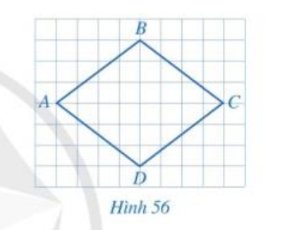
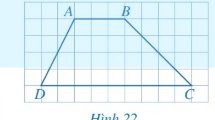
Hai cạnh AB và CD của tứ giác ABCD có song song với nhau.

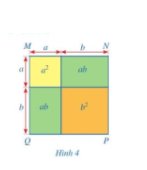
Cách 1: Diện tích hình vuông MNPQ là: \({a^2} + ab + ab + {b^2} = {a^2} + 2{\rm{a}}b + {b^2}\)
Cách 2: Độ dài cạnh của hình vuông MNPQ là: \(a + b\)
Diện tích của hình vuông MNPQ là: \(\left( {a + b} \right).\left( {a + b} \right) = {\left( {a + b} \right)^2}\)

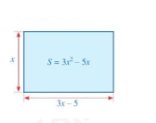
\(3{{\rm{x}}^2} - 5{\rm{x = x}}\left( {3{\rm{x}} - 5} \right)\)

Những hình khối có dạng ở hình 11 được gọi là hình chóp tứ giác đều.

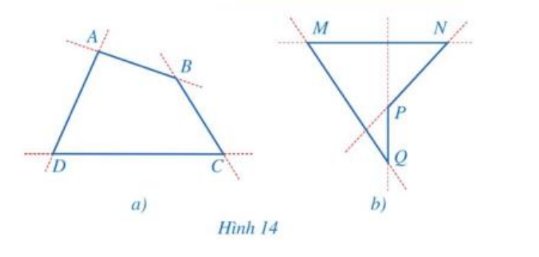
Hình 14a: Tứ giác ABCD luôn nằm về 1 phía của 1 cạnh bất kì.
Hình 14b: Tứ giác MNPQ nằm về 2 phía của đường thẳng chứa cạnh PQ, cạnh NP
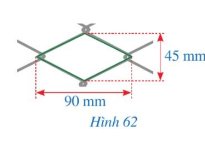


Giả sử mắt lưới cần tính độ dài cạnh là hình thoi ABCD.
Có. AC = 45mm; BD = 90mm.
Gọi O là giao điểm của AC và BD.
Vì ABCD là hình thoi nên
\(\begin{array}{l}OA = OC = \dfrac{{AC}}{2} = \dfrac{{45}}{2} = 22,5(mm)\\OB = OD = \dfrac{{BD}}{2} = \dfrac{{90}}{2} = 45(mm)\end{array}\)
Xét \(\Delta AOB\) vuông tại O có:
\(\begin{array}{l}A{O^2} + O{B^2} = A{B^2}\\{(22,5)^2} + {(45)^2} = A{B^2} \Rightarrow A{B^2} = 2.531,25 \Rightarrow AB \approx 50(mm)\end{array}\)