Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

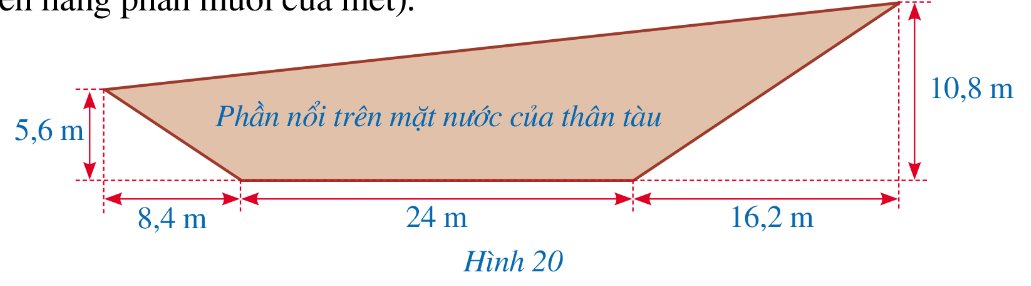
*) Áp dụng định lí Pythagore trong tam giác \(\Delta ABC\) vuông tại A có
\(A{C^2} = A{B^2} + B{C^2} = 5,{6^2} + 8,{4^2} = 101,92 \Rightarrow AC = \sqrt {101,92} \)
\(\Delta DEF\) vuông tại F có
\(D{F^2} = D{E^2} + E{F^2} = 16,{2^2} + 10,{8^2} = 379,08 \Rightarrow DF = \sqrt {379,08} \)
Kẻ \(AG \bot FG\)
Khi đó: \(FG = FE - GE = FE - AB = 10,8 - 5,6 = 5,2\)
Áp dụng định lí Pythagore trong \(\Delta AGF\) vuông tại G có
\(A{F^2} = A{G^2} + F{G^2} = 48,{6^2} + 5,{2^2} = 2389 \Rightarrow AF = \sqrt {2389} \)
Chu vi tứ giác ACDF là:
\(AC + CD + DF + AF = \sqrt {101,92} + \sqrt {379,08} + 24 + \sqrt {2389} \approx 102,4\)
Vậy chu vi của mặt cắt dọc phần nổi trên mặt nước của chiếc tàu thủy là khoảng 102,4m.

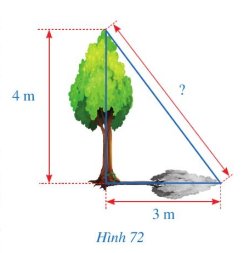
Khoảng cách từ điểm xa nhất của bóng cây đến đỉnh cây bằng \(\sqrt{3^2+4^2}=5\left(m\right)\) (áp dụng định lý Py-ta-go).

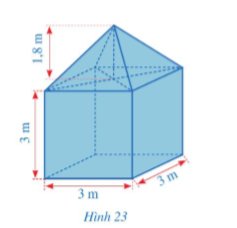
Thể tích của lều trại đó là.
\(V = {3^3} + \dfrac{1}{3}{3^2}.1,8 = 32,4({m^3})\)

Áp dụng định lí Py-ta-go, ta có:
\(2,1^2+h^2=3,5^2\\ \Leftrightarrow h=\sqrt{3,5^2-2,1^2}=2,8m\)

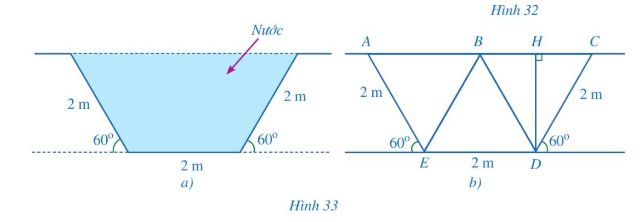
a, Do ACDE là hình thang cân nên
AC//DE suy ra AB//ED \( \Rightarrow {{\widehat B} _1} = {{\widehat E} _3},{{\widehat A} _1} = {{\widehat E} _1} = {60^0};{{\widehat C} _1} = {{\widehat D} _1} = {60^0}\)
Mà: AE//BD \( \Rightarrow {{\widehat B} _2} = {{\widehat E} _2}\)
Xét \(\Delta ABE\) và \(\Delta B{\rm{D}}E\) có: \({{\widehat B} _1} = {{\widehat E} _3}\) ; BE chung
\(\begin{array}{l}{{{\widehat B} }_2} = {{{\widehat E} }_2} \Rightarrow \Delta ABE = \Delta B{\rm{D}}E \Rightarrow A{\rm{E}} = B{\rm{D}} = 2m.\\AB = E{\rm{D}} = 2m\end{array}\)
Xét \(\Delta BC{\rm{D}}\) có \({{\widehat C} _1} = {60^0};B{\rm{D}} = C{\rm{D}} = 2m \Rightarrow \Delta BC{\rm{D}}\) đều.
Xét \(\Delta A{\rm{E}}B\) có \({{\widehat A} _1} = {60^0};AB = A{\rm{E}} = 2m \Rightarrow \Delta A{\rm{E}}B\) đều.
Vì: \(\Delta A{\rm{E}}B\) đều suy ra: BE = 2 m.
Xét \(\Delta BE{\rm{D}}\) có BD = BE = ED = 2m \( \Rightarrow \Delta BE{\rm{D}}\) đều.
b, Vì \(\Delta ABE,\Delta BC{\rm{D}}\) là các tam giác đều nên AB = BC = 2m.
Suy ra AC = AB + BC = 4m.
Do \(\Delta B{\rm{D}}C\) đều nên H là trung điểm của BC.
Suy ra HC = HB =\(\dfrac{{BC}}{2} = 1\)
Xét \(\Delta DHC\) vuông tại H ta có:
\(D{C^2} = D{H^2} + H{C^2}\) (theo định lý pythagore)
\(\begin{array}{l} \Rightarrow D{H^2} = D{C^2} - H{C^2} = {2^2} - {1^2} = 3\\ \Rightarrow DH = \sqrt 3 \end{array}\)
c, Diện tích hình thang cân AEDC là:
\({S_{A{\rm{ED}}C}} = \dfrac{1}{2}DH.(AC + E{\rm{D}}) = \dfrac{1}{2}\sqrt 3 (2 + 4) = 3\sqrt 3 (c{m^2})\)
Vậy diện tích mặt cắt phần chứa nước: \(3\sqrt 3 c{m^2}\)

Diện tích xung quanh của mái che giếng trời là.
\({S_{xq}} = \dfrac{1}{2}(2,2.4).2,8 = 12,32({m^2})\)
Số tiền cần phải trả để làm mái che giếng trời là.
1800000.12,32 = 22 176 000 (đồng)

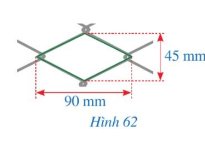
Giả sử mắt lưới cần tính độ dài cạnh là hình thoi ABCD.
Có. AC = 45mm; BD = 90mm.
Gọi O là giao điểm của AC và BD.
Vì ABCD là hình thoi nên
\(\begin{array}{l}OA = OC = \dfrac{{AC}}{2} = \dfrac{{45}}{2} = 22,5(mm)\\OB = OD = \dfrac{{BD}}{2} = \dfrac{{90}}{2} = 45(mm)\end{array}\)
Xét \(\Delta AOB\) vuông tại O có:
\(\begin{array}{l}A{O^2} + O{B^2} = A{B^2}\\{(22,5)^2} + {(45)^2} = A{B^2} \Rightarrow A{B^2} = 2.531,25 \Rightarrow AB \approx 50(mm)\end{array}\)

Gọi A là đỉnh hình chóp và BC là 1 cạnh đáy (BC = 2,2m) tạo thành tam giác ABC cân tại A, AH là đường cao kẻ từ A xuống BC (H thuộc BC và AH = 2,8m)
=> AH đồng thời là đường trung trực của BC
=> H là trung điểm BC => BH = BC/2 = 2,2/2 = 1,1 (m)
Xét tam giác ABH vuông tại H (AH vuông góc với BC)
=> AB = \(\sqrt{BH^2+AH^2}\) = \(\sqrt{1,1^2+2,8^2}\) = 6,5 (m)
Vậy độ dài cạnh bên khoảng 6,5 m

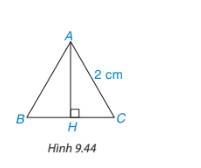
Vì tam giác ABC là tam giác đều, \(AH \bot BC\) nên H là trung điểm của BC suy ra
\(HB = HC = \frac{{BC}}{2} = \frac{2}{2} = 1\)(cm)
Áp đụng định lí Pythagore trong tam giác AHC ta có:
\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2} \Rightarrow A{H^2} = A{C^2} - H{C^2} = {2^2} - {1^2} = 3\\ \Rightarrow AH = \sqrt 3 \approx 1,73(cm)\end{array}\)
Vậy chiều cao của tam giác đều là 1,73cm.
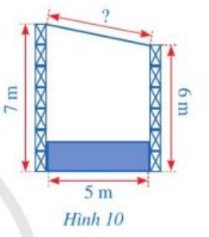



Gọi CB là chiều dài của mái che sân khấu. AB = 7- 6 = 1m, AC = 5m.
Từ C kẻ đường thẳng vuông góc với khung trước của sân khấu tại A. Ta có \( \Delta ABC \) vuông tại A.
Áp dụng định lí Pythagore trong tam giác vuông tại A. ta có:
\(C{B^2} = A{C^2} + A{B^2} = {1^2} + {5^2} = 26 \Rightarrow CB = \sqrt {26} = 5,10(m)\)