Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đồ thị hàm số y = sin x trên đoạn [-2π, 2π]
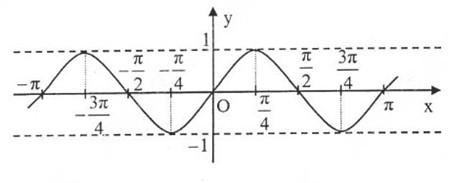
Dựa vào đồ thị hàm số y = sinx
a) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị bằng -1 là:
x=−π2;x=3π2x=−π2;x=3π2
b) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị âm là:
x ∈ (-π, 0) ∪ (π, 2 π)

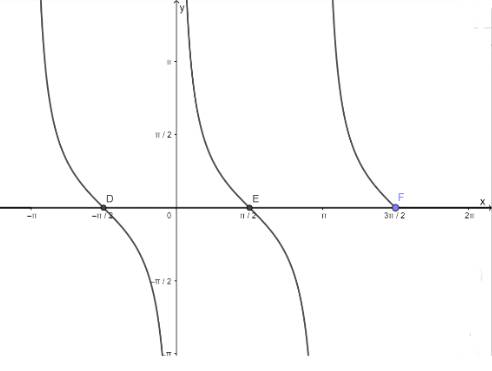
Quan sát đồ thị hàm số y = tan x trên đoạn [-π; 3π/2].
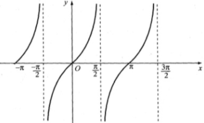
a. tan x = 0 tại các giá trị x = -π; 0; π.
(Các điểm trục hoành cắt đồ thị hàm số y = tanx).
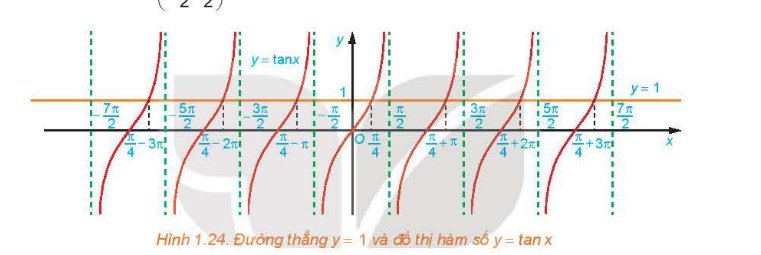
b. tan x = 1 tại các giá trị x = -3π/4; π/4; 5π/4.
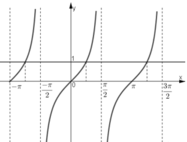
c. tan x > 0 với x ∈ (-π; -π/2) ∪ (0; π/2) ∪ (π; 3π/2).
(Quan sát hình dưới)
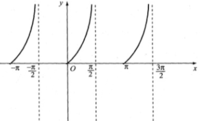
d. tan x < 0 khi x ∈ [-π/2; 0) ∪ [π/2; π)
(Quan sát hình dưới).
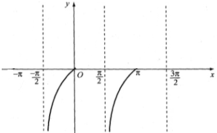

Hàm số nhận giá trị âm ứng với phần đồ thị nằm dưới trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \pi ;\frac{{3\pi }}{2}} \right]\), thì \(y < 0\) khi \(x\; \in \left( { - \frac{\pi }{2};0} \right) \cup \left( {\frac{\pi }{2};\;\pi } \right)\)

Hàm số nhận giá trị dương ứng với phần đồ thị nằm trên trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\), thì \(y > 0\) khi \(x\; \in \left( {0;\frac{\pi }{2}} \right) \cup \left( {\;\pi ;\frac{{3\pi }}{2}} \right)\)

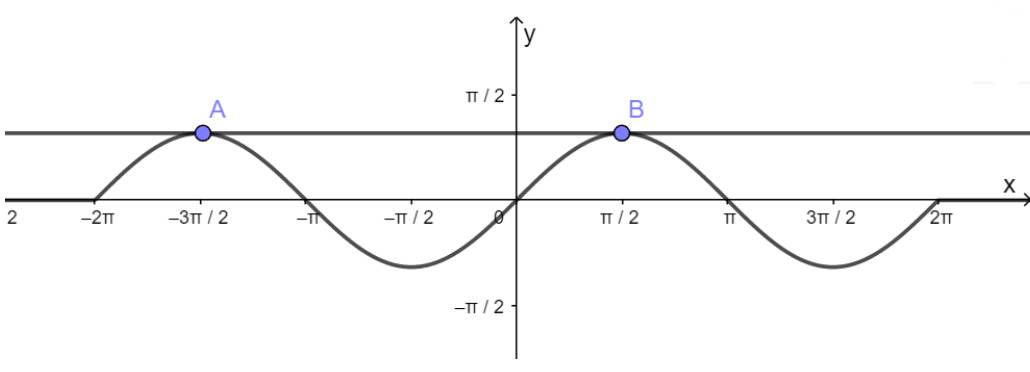
a) Hàm số y = sinx nhận giá trị bằng 1
- Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 1
- Lấy giao điểm của hai hàm số y = sinx và y = 1 là A, B,...
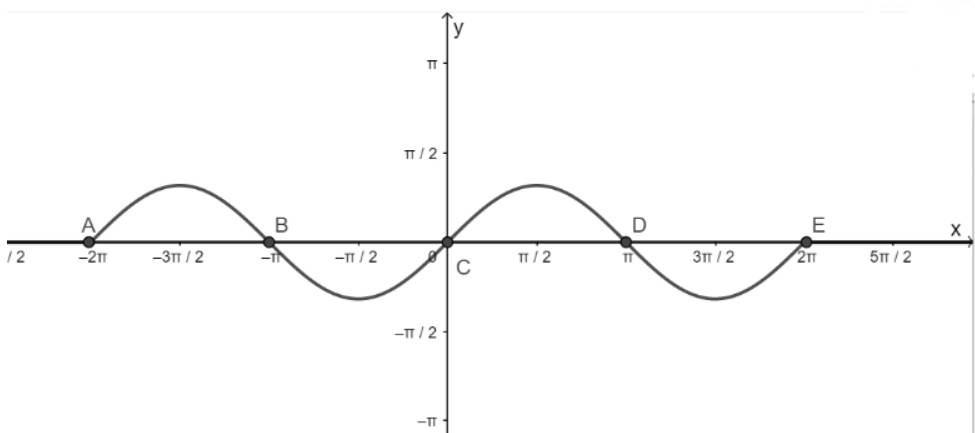
b) Hàm số y = sinx nhận giá trị bằng 0
- Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = sinx và y = 0 là A, B, C, D, E,...
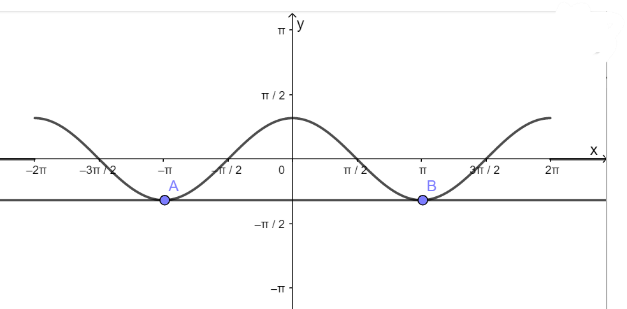
c) Hàm số y = cosx nhận giá trị bằng – 1
- Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = - 1
- Lấy giao điểm của hai hàm số y = cosx và y = - 1 là A, B,...
d) Hàm số y = cosx nhận giá trị bằng 0
- Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = cosx và y = 0 là C, D, E, F,...
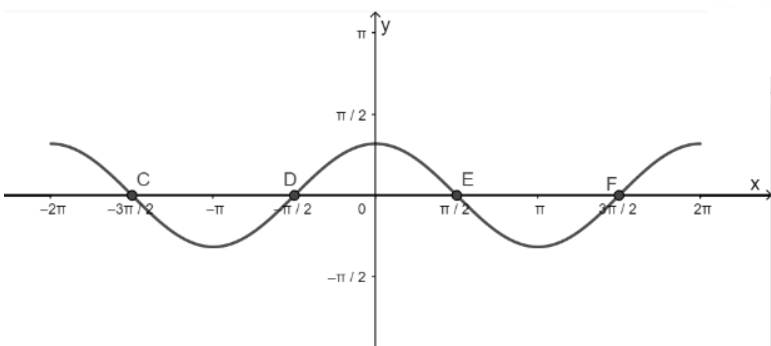

a) Hàm số y = tanx nhận giá trị bằng – 1
- Vẽ hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = - 1
- Lấy giao điểm của hai hàm số y = tanx và y = - 1
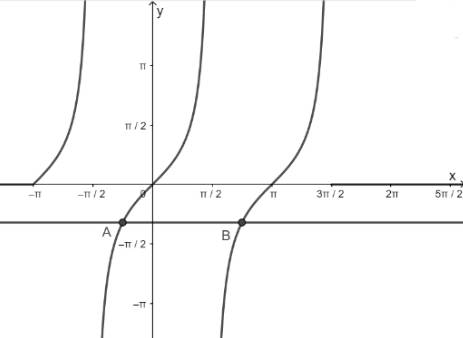
b) Hàm số y = tanx nhận giá trị bằng 0
- Vẽ hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = tanx và y = 0
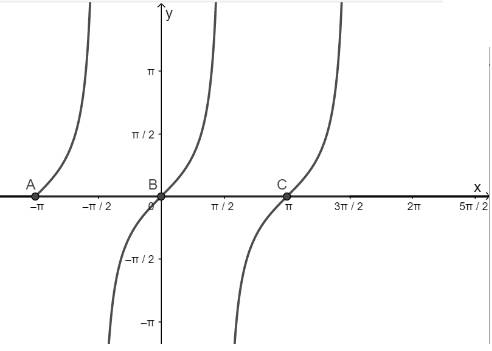
c) Hàm số y = cotx nhận giá trị bằng 1
- Vẽ hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 1
- Lấy giao điểm của hai hàm số y = cotx và y = 1
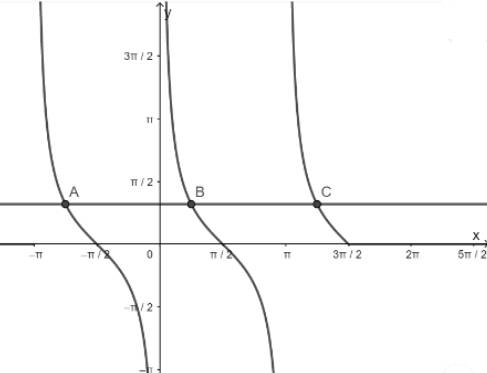
d) Hàm số y = cotx nhận giá trị bằng 0
- Vẽ hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = tanx và y = 0

Bài 6. Các giá trị cần tìm của x là các nghiệm của phương trình
tan 2x = tan (![]() - x) ,
- x) ,
Đáp số : ![]() ( k ∈ Z, k - 2 không chia hết cho 3).
( k ∈ Z, k - 2 không chia hết cho 3).
Giá trị của x cần tìm là nghiệm của phương trình:
\(tan\left(\dfrac{\pi}{4}-x\right)=tan2x\)
pt\(\Leftrightarrow\left\{{}\begin{matrix}cos\left(\dfrac{\pi}{4}-x\right)\ne0\\cos2x\ne0\\\dfrac{\pi}{4}-x=2x+k\pi\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}cos2x\ne0\\3x=\dfrac{\pi}{4}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x\ne\dfrac{\pi}{2}+k\pi\\x=\dfrac{\pi}{12}+\dfrac{k\pi}{3}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x=\dfrac{\pi}{12}+\dfrac{k\pi}{3}\end{matrix}\right.\)\(\Leftrightarrow x=\dfrac{\pi}{12}+\dfrac{k\pi}{3}\).
Bài 1. a) trục hoành cắt đoạn đồ thị y = tanx (ứng với x ∈.gif) ) tại ba điểm có hoành độ - π ; 0 ; π. Do đó trên đoạn
) tại ba điểm có hoành độ - π ; 0 ; π. Do đó trên đoạn .gif) chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 0, đó là x = - π; x = 0 ; x = π.
chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 0, đó là x = - π; x = 0 ; x = π.
b) Đường thẳng y = 1 cắt đoạn đồ thị y = tanx (ứng với x ∈.gif) ) tại ba điểm có hoành độ
) tại ba điểm có hoành độ .gif) . Do đó trên đoạn
. Do đó trên đoạn .gif) chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 1, đó là
chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 1, đó là .gif) .
.
c) Phần phía trên trục hoành của đoạn đồ thị y = tanx (ứng với x ∈.gif) ) gồm các điểm của đồ thị có hoành độ truộc một trong các khoảng
) gồm các điểm của đồ thị có hoành độ truộc một trong các khoảng .gif) . Vậy trên đoạn
. Vậy trên đoạn .gif) , các giá trị của x để hàm số y = tanx nhận giá trị dương là x ∈
, các giá trị của x để hàm số y = tanx nhận giá trị dương là x ∈ .png) .
.
d) Phần phía dưới trục hoành của đoạn đồ thị y = tanx (ứng với x ∈.gif) ) gồm các điểm của đồ thị có hoành độ thuộc một trong các khoảng
) gồm các điểm của đồ thị có hoành độ thuộc một trong các khoảng .png) . Vậy trên đoạn
. Vậy trên đoạn .gif) , các giá trị của x để hàm số y = tanx nhận giá trị âm là x ∈
, các giá trị của x để hàm số y = tanx nhận giá trị âm là x ∈ .png) .
.
a) \(\left\{-\pi;0;\pi\right\}\)
b) \(\left\{\dfrac{\pi}{4};\dfrac{\pi}{4}\pm\pi\right\}\)
c) \(\left(-\pi;-\dfrac{\pi}{2}\right)\cup\left(0;\dfrac{\pi}{2}\right)\cup\left(\pi;\dfrac{3\pi}{2}\right)\)
d) \(\left(-\dfrac{\pi}{2};0\right)\cup\left(\dfrac{\pi}{2};\pi\right)\)