KT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 10 2021
a: \(x^4+3x^3+x^2+3x\)
\(=x\left(x^3+3x^2+x+3\right)\)
\(=x\left(x+3\right)\left(x^2+1\right)\)
c: \(x^2-xy-x+y\)
\(=x\left(x-y\right)-\left(x-y\right)\)
\(=\left(x-y\right)\left(x-1\right)\)
TL
1
8 tháng 1 2022
a) x2+x-2
= x2-x+2x-2
= x(x-1)+2(x-1)
= (x+2)(x-1)
b) 2x2+5x+3
= 2x2+2x+3x+3
= 2x(x+1)+3(x+1)
= (2x+3)(x+1)
c) 3x2+5x-2
= 3x2+6x-1x-2
= 3x(x+2)-1(x+2)
= (3x-1)(x+2)
TD
2
28 tháng 7 2021
\(x-y=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)\)
TL
1
5 tháng 11 2021
a: \(=25x^2-4y^2+4y-1\)
\(=25x^2-\left(2y-1\right)^2\)
\(=\left(5x-2y+1\right)\left(5x+2y-1\right)\)
NG
2
9 tháng 6 2019
(3-x)4+(4-x)4-(7-2x)4
Đặt 3-x=a, 4-x=b=> 7-2x=a+b
=> (3-x)4+(4-x)4-(7-2x)4
=a4+b4-(a+b)4
=-(4a3b+6a2b2+4ab3)
=-2ab(a2+3ab+b2)
TL
2
26 tháng 11 2021
\(a,=\left(2y^2-1\right)\left(2y^2+1\right)\\ b,=\left(x+y\right)^2-9=\left(x+y+3\right)\left(x+y-3\right)\)
AH
Akai Haruma
Giáo viên
26 tháng 11 2021
Lời giải:
a. $4y^4-1=(2y^2)^2-1^2=(2y^2-1)(2y^2+1)$
b. $x^2+2xy-9+y^2=(x^2+2xy+y^2)-9$
$=(x+y)^2-3^2=(x+y-3)(x+y+3)$
31 tháng 8 2021
\(x^4-x^3-x+1=\left(x^4-x^3\right)-\left(x-1\right)=x^3\left(x-1\right)-\left(x-1\right)=\left(x^3-1\right)\left(x-1\right)=\left(x-1\right)^2.\left(x^2+x+1\right)\)
KK
31 tháng 8 2021
x4 - x3 - x + 1
= (x4 - x3) - (x - 1)
= x3(x - 1) - (x - 1)
= (x3 - 1)(x - 1)
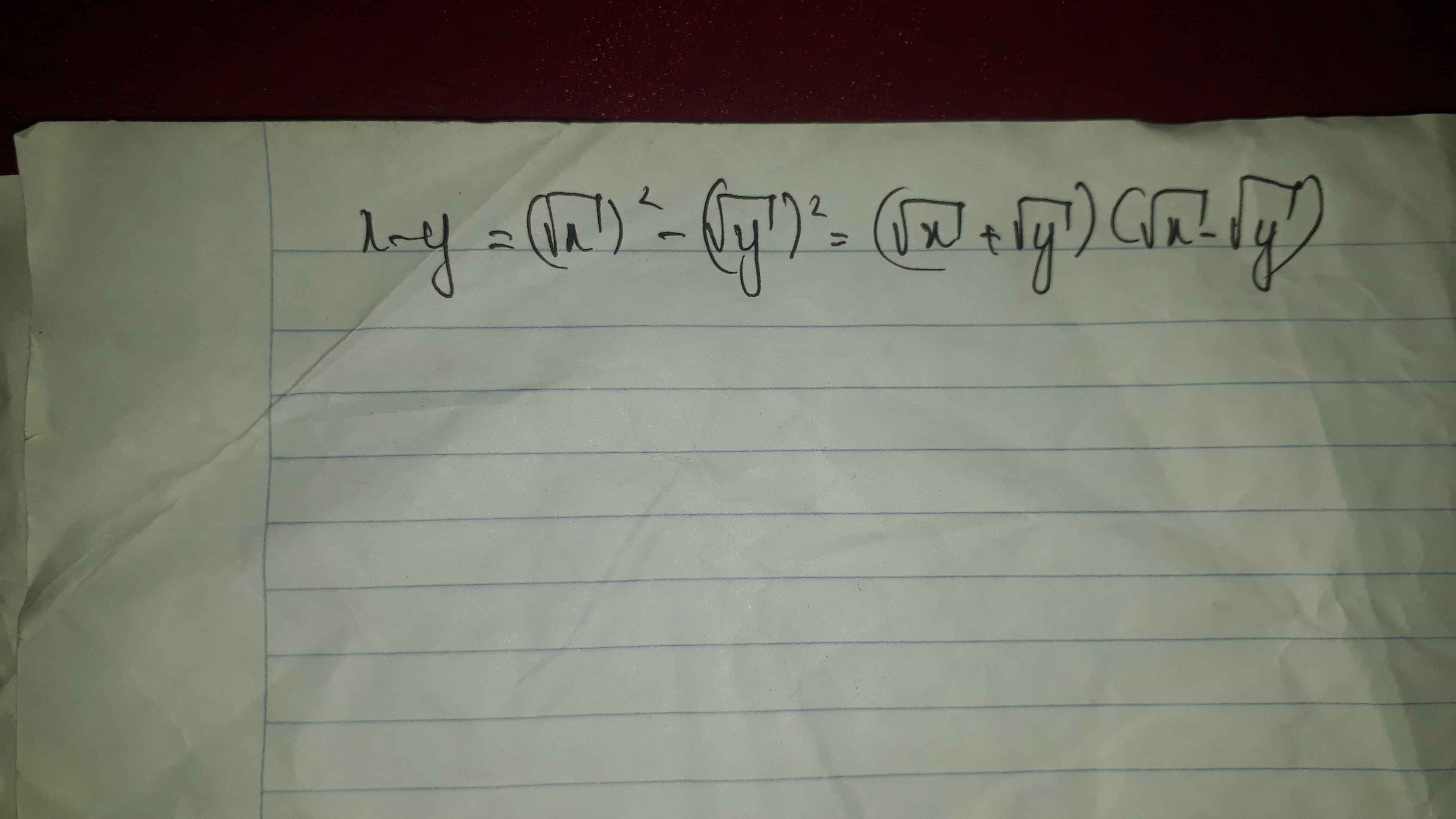
a) = x * x * x * x * x * x *x *x * x * x * x
x^11+x^4+1
=x^11-x^2+x^4-x+x^2+x+1
=x^2(x^9-1)+x(x^3-1)+(x^2+x+1)
=x^2[(x^3-1)(x^6+x^3+1)]+x(x-1)(x^2+x+1)+(x^2+x+1)
=x^2(x-1)(x^2+x+1)(x^6+x^3+1)+x(x-1)(x^2+x+1)+(x^2+x+1)
=(x^2+x+1)[x^2(x-1)(x^6+x^3+1)+x(x-1)+1]
=(x^2+x+1)(x^9-x^8+x^6-x^5+x^3-x+1)