Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\)\(\sqrt{x^2-2x+1}=\sqrt{\left(x-1\right)^2}\)
\(đkxđ\Leftrightarrow\sqrt{\left(x-1\right)^2}\ge0\)
\(\Rightarrow x-1\ge0\Rightarrow x\ge1\)
\(b,\)\(\sqrt{x+3}+\sqrt{x+9}\)
\(đkxđ\Leftrightarrow\hept{\begin{cases}x+3\ge0\\x+9\ge0\end{cases}\Rightarrow\hept{\begin{cases}x\ge-3\\x\ge-9\end{cases}}}\)
\(\Rightarrow x\ge-3\)
\(c,\)\(\sqrt{\frac{x-1}{x+2}}\)
\(đkxđ\Leftrightarrow\hept{\begin{cases}x+2\ne0\\\frac{x-1}{x+2}\ge0\end{cases}\Rightarrow\hept{\begin{cases}x\ne-2\\\frac{x-1}{x+2}\ge0\end{cases}}}\)
\(\frac{x-1}{x+2}\ge0\)\(\Rightarrow\orbr{\begin{cases}x-1\ge0;x+2>0\\x-1\le0;x+2< 0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x\ge-1;x>-2\\x\le1;x< 2\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x\ge-1\\x< 2\end{cases}}\)
Vậy căn thức xác định khi x \(\ge\)-1 hoawck x < 2

Ta có:
x 2 + 2 13 x + 13 = x 2 + 2 . x . 13 + 13 2 = x + 13 2

a) \(x^2-5=\left(x-\sqrt{5}\right)\left(x+\sqrt{5}\right)\)
b) \(x^2-11=\left(x-\sqrt{11}\right)\left(x+\sqrt{11}\right)\)
c: \(x-2=\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\)
d: \(x^2-2\sqrt{5x}+5=\left(x-\sqrt{5}\right)^2\)

a: \(13\sqrt{11}=\sqrt{13^2\cdot11}=\sqrt{1859}\)
b: \(-8\sqrt{2}=-\sqrt{64\cdot2}=-\sqrt{128}\)
c: \(a\sqrt{5a}=\sqrt{a^2\cdot5a}=\sqrt{5a^3}\)
d: \(b\sqrt{\dfrac{5}{ab}}=-\sqrt{b^2\cdot\dfrac{5}{ab}}=-\sqrt{\dfrac{5b}{a}}\)

a ) x 2 - 3 = x 2 - ( √ 3 ) 2 = ( x - √ 3 ) ( x + √ 3 ) b ) x 2 - 6 = x 2 - ( √ 6 ) 2 = ( x - √ 6 ) ( x + √ 6 ) c ) x 2 + 2 √ 3 x + 3 = x 2 + 2 √ 3 x + ( √ 3 ) 2 = ( x + √ 3 ) 2 d ) x 2 - 2 √ 5 x + 5 = x 2 - 2 √ 5 x + ( √ 5 ) 2 = ( x - √ 5 ) 2

3x2 + 8x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ’ = 42 – 2.3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:

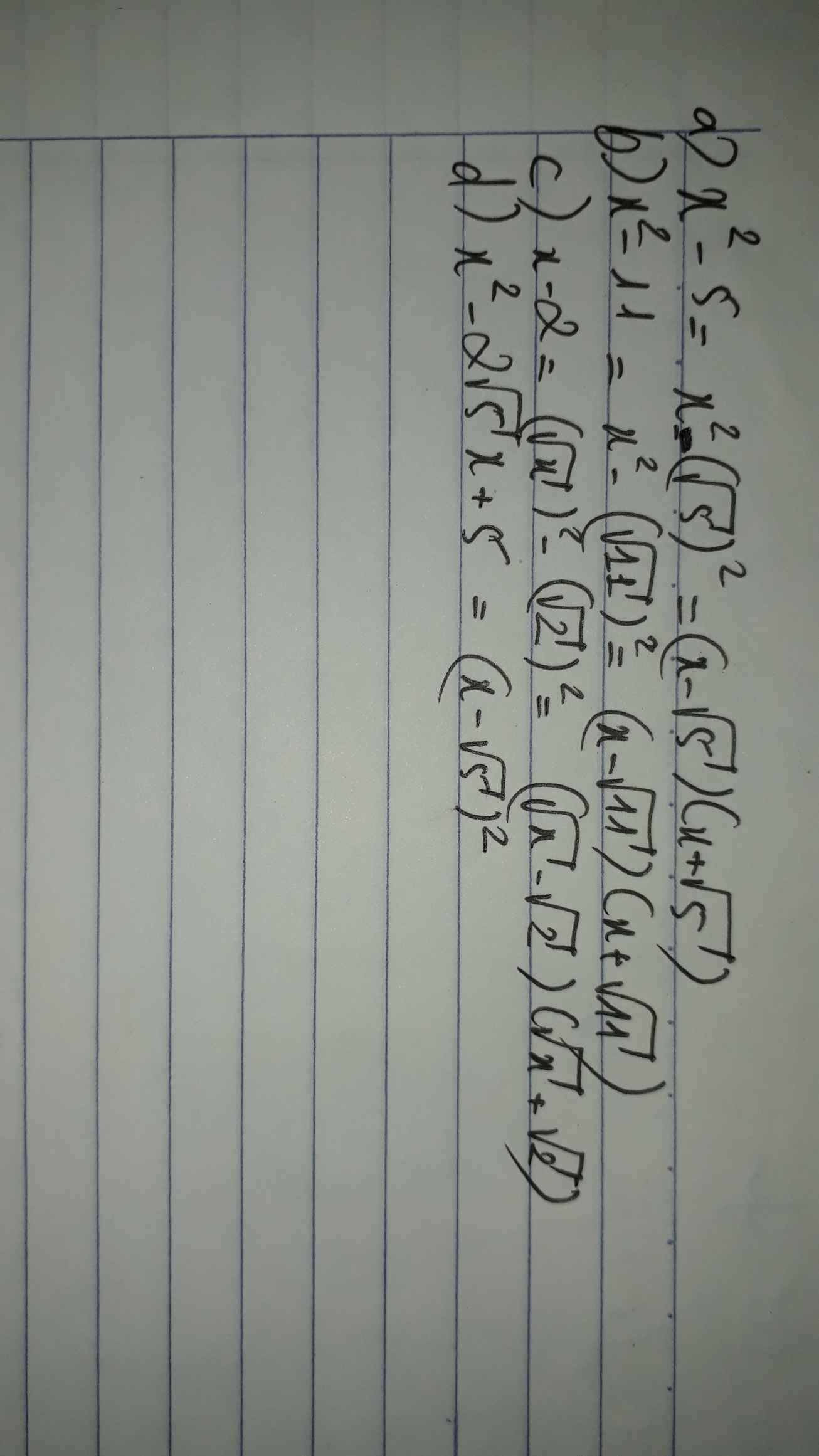
a, x2-7=\(\left(x-\sqrt{7}\right)\left(x+\sqrt{7}\right)\)
b, x2-3=\(\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)\)
Học tốt!!!!!!!!!!
a/ \(x^2-7\)
\(=\left(x-\sqrt{7}\right)\left(x+\sqrt{7}\right)\)
b/ \(x^2-3\)
\(=\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)\)
c/ \(x^2-2\sqrt{13}x+13\)
\(=\left(x-\sqrt{13}\right)^2\)
Mấy bài này áp dụng HĐT nhé bạn :3