
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,10x^2y-20xy^2=10xy\left(x-2y\right)\\ b,x^2-y^2+10y-25=x^2-\left(y^2-10y+25\right)=x^2-\left(y-5\right)^2=\left(x-y+5\right)\left(x+y-5\right)\\ c,x^2-y^2+3x-3y=\left(x-y\right)\left(x+y\right)+3\left(x-y\right)=\left(x-y\right)\left(x+y+3\right)\\ d,x^3+3x^2-16x-48=\left(x^3+3x^2\right)-\left(16x+48\right)=x^2\left(x+3\right)-16\left(x+3\right)=\left(x+3\right)\left(x^2-16\right)=\left(x+3\right)\left(x+4\right)\left(x-4\right)\)
\(e,9x^3+6x^2+x=x\left(9x^2+6x+1\right)=x\left(3x+1\right)^2\\ f,x^4+5x^3+15x-9=\left(x^4+5x^3-3x^2\right)+\left(3x^2+15x-9\right)=x^2\left(x^2+5x-3\right)+3\left(x^2+5x-3\right)=\left(x^2+3\right)\left(x^2+5x-3\right)\)

Lời giải:
a.
$3x^2+xy-4y^2=(3x^2-3xy)+(4xy-4y^2)=3x(x-y)+4y(x-y)=(x-y)(3x+4y)$
b.
$x^8-5x^4+4=(x^8-x^4)-(4x^4-4)$
$=x^4(x^4-1)-4(x^4-1)=(x^4-1)(x^4-4)$
$=(x^2-1)(x^2+1)(x^2-2)(x^2+2)$
$=(x-1)(x+1)(x^2+1)(x-\sqrt{2})(x+\sqrt{2})(x^2+2)$
c.
$x^3+3x^2+3x-7=(x^3+3x^2+3x+1)-8$
$=(x+1)^3-2^3=(x+1-2)[(x+1)^2+2(x+1)+4]$
$=(x-1)(x^2+4x+7)$
a) \(3x^2+xy-4y^2=3x^2-3xy+4xy-4y^2\)
\(=3x(x-y)+4y(x-y)=(3x+4y)(x-y)\)
b)\(x^8-5x^4+4=x^8-x^4-4x^4+4\)
\(=x^2(x^4-1)-4(x^4-1)=(x^2-4)(x^4-1)\)
\(=(x-2)(x+2)(x^2-1)(x^2+1)=(x-2)(x+2)(x-1)(x+1)(x^2+1)\)
c)\(x^3+3x^2+3x-7=x^3+3x^2+3x+1-8\)
\(\left(x+1\right)^3-\sqrt{2}^3=\left(x+1-\sqrt[]{2}\right)\left(\left(x+1\right)^2+2\sqrt{2}x+2\right)\)

1a) \(=-\left(x^3-3x^2+3x-1\right)=-\left(x-1\right)^3\)
b) \(=-\left(x^3-3x^2+3x-1\right)=-\left(x-1\right)^3\)
\(a,=-\left(x-1\right)^3\left[=\left(1-x\right)^3\right]\\ b,=\left(1-x\right)^3\)

a: \(=\left(2x+y\right)^2-3^2=\left(2x+y+3\right)\left(2x+y-3\right)\)
b: =3x(x-y)-(x-y)=(x-y)(3x-1)

\(2a\left(x^2-9\right)=2a\left(x-3\right)\left(x+3\right)\)

a) x3+4x-5 = x3-x2+x2+4x-5=(x3-x2)+(x2-x)+(5x-5)=x2(x-1)+x(x-1)+5(x-1)=(x2+x+5)(x-1)
b) x3-3x2+4=x3-2x2-x2+4=(x3-2x2)-(x2-4)=x2(x-2)-(x-2)(x+2)=(x2-x+2)(x-2)
c) x3+2x2+3x+2=x3+x2+x2+x+2x+2=(x3+x2)+(x2+x)+(2x+2)=x2(x+1)+x(x+1)+2(x+1)=(x2+x+2)(x+1)
d) bạn xem lại đề đúng ko
e) (x2+3x)2-2(x2+3x)-8=x4+6x3+9x2-2x2-6x-8=x4+6x3+7x2-6x-8=x4-x3+7x3-7x2+14x2-14x+8x-8=(x4-x3)+(7x3-7x2)+(14x2-14x)+(8x-8)=x3(x-1)+7x2(x-1)+14x(x-1)+8(x-1)=(x3+7x2+14x+8)(x-1)=(x3+x2+6x2+6x+8x+8)(x-1)=\(\left[\left(x^3+x^2\right)+\left(6x^2+6x\right)+\left(8x+8\right)\right]\left(x-1\right)\)\(=\left[x^2\left(x+1\right)+6x\left(x+1\right)+8\left(x+1\right)\right]\left(x-1\right)\)\(=\left(x^2+6x+8\right)\left(x+1\right)\left(x-1\right)\)\(=\left(x^2+2x+4x+8\right)\left(x+1\right)\left(x-1\right)\)\(=\left[\left(x^2+2x\right)+\left(4x+8\right)\right]\left(x+1\right)\left(x-1\right)\)\(=\left[x\left(x+2\right)+4\left(x+2\right)\right]\left(x+1\right)\left(x-1\right)\)=\(\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x+4\right)\)
f) (x2+4x+10)2-7(x2+4x+11)+7=(x2+4x+10)2-\(\left[7\left(x^2+4x+11\right)-7\right]\)\(=\left(x^2+4x+10\right)^2-7\left(x^2+4x+10\right)\)\(=\left(x^2+4x+10\right)\left(x^2+4x+3\right)\)
a) Ta có: \(x^3+4x-5\)
\(=x^3-x+5x-5\)
\(=x\left(x-1\right)\left(x+1\right)+5\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2+x+5\right)\)
b) Ta có: \(x^3-3x^2+4\)
\(=x^3+x^2-4x^2+4\)
\(=x^2\left(x+1\right)-4\left(x-1\right)\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2-4x+4\right)\)
\(=\left(x+1\right)\cdot\left(x-2\right)^2\)
c) Ta có: \(x^3+2x^2+3x+2\)
\(=x^3+x^2+x^2+x+2x+2\)
\(=x^2\left(x+1\right)+x\left(x+1\right)+2\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2+x+2\right)\)
d) Ta có: \(x^2+2xy+y^2+2x+2y-3\)
\(=\left(x+y\right)^2+2\left(x+y\right)-3\)
\(=\left(x+y\right)^2+3\left(x+y\right)-\left(x+y\right)-3\)
\(=\left(x+y\right)\left(x+y+3\right)-\left(x+y+3\right)\)
\(=\left(x+y+3\right)\left(x+y-1\right)\)

\(g,x^4-16=\left(x^2-4\right)\left(x^2+4\right)=\left(x-2\right)\left(x+2\right)\left(x^2+4\right)\\ i,-x^2+10x-25=-\left(x-5\right)^2\\ k,x^3+3x^2+3x+1-27z^3\\ =\left(x+1\right)^3-27z^3\\ =\left(x+1-3z\right)\left[\left(x+1\right)^2+3z\left(x+1\right)+9z^2\right]\\ =\left(x-3z+1\right)\left(x^2+2x+1+3xz+3z+9z^2\right)\\ m,\left(x+y\right)^2-25\left(x+y\right)+24=\left(x+y-5\right)^2-1=\left(x+y-4\right)\left(x+y-6\right)\)
g. x4 - 16
<=> x4 - 42
<=> (x2)2 - 42
<=> (x2 - 4)(x2 + 4)
i. -x2 + 10x - 25
<=> -(x2 - 10x + 25)
<=> -(x2 -10x + 52)
<=> -(x - 5)2

`a)x^3-8x^2+16x`
`=x(x^2-8x+16)`
`=x(x-4)^2`
`b)x^2+4y^2+2x-4y-4xy-24`
`=(x-2y)^2+2(x-2y)-24`
`=(x-2y)^2-4(x-2y)+6(x-2y)-24`
`=(x-2y-4)(x-2y+6)`
`c)x^4+x^3-x^2-2x-2`
`=x^4-2x^2+x^3-2x+x^2-2`
`=x^2(x^2-2)+x(x^2-2)+x^2-2`
`=(x^2-2)(x^2+x+1)`

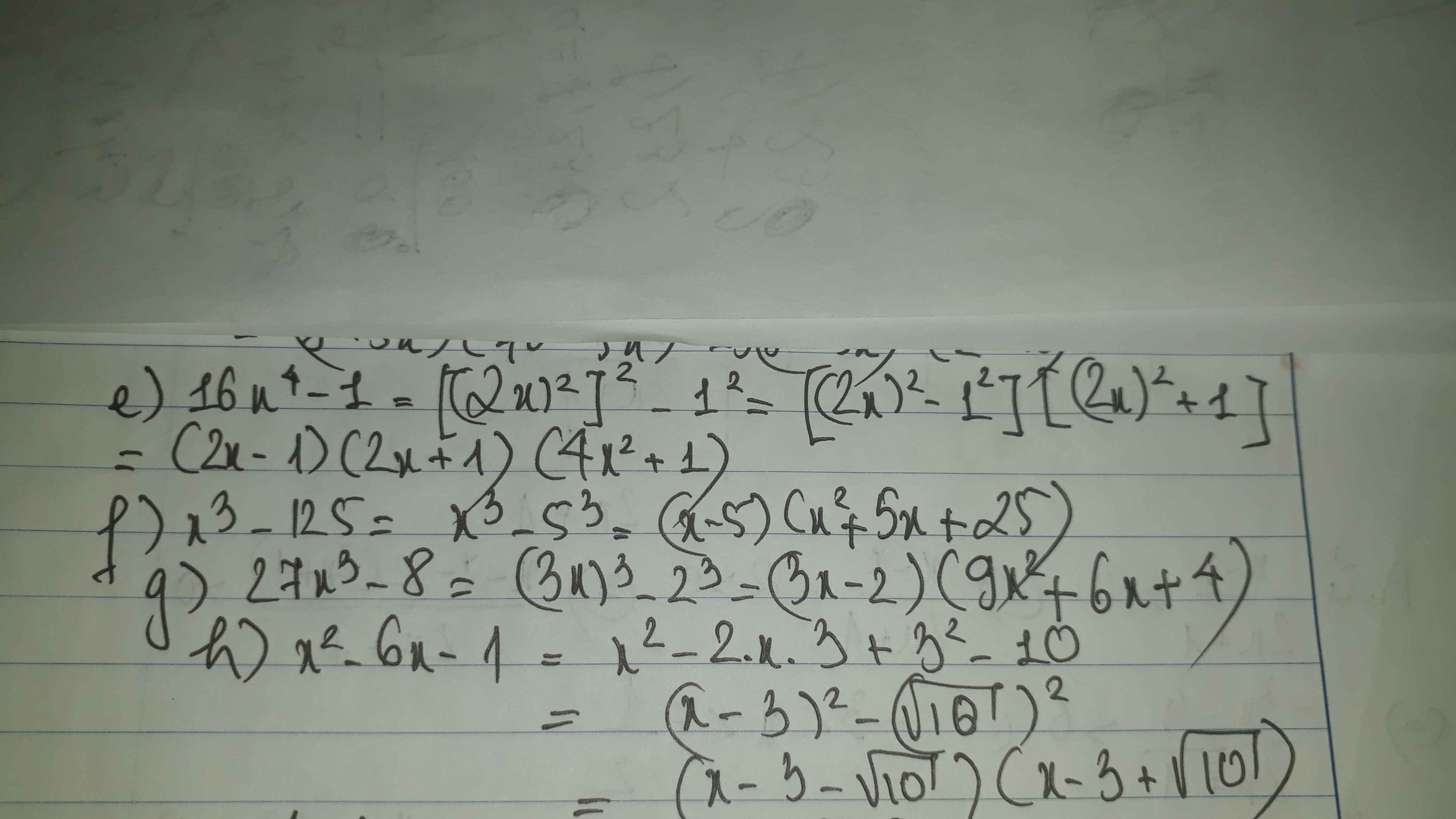
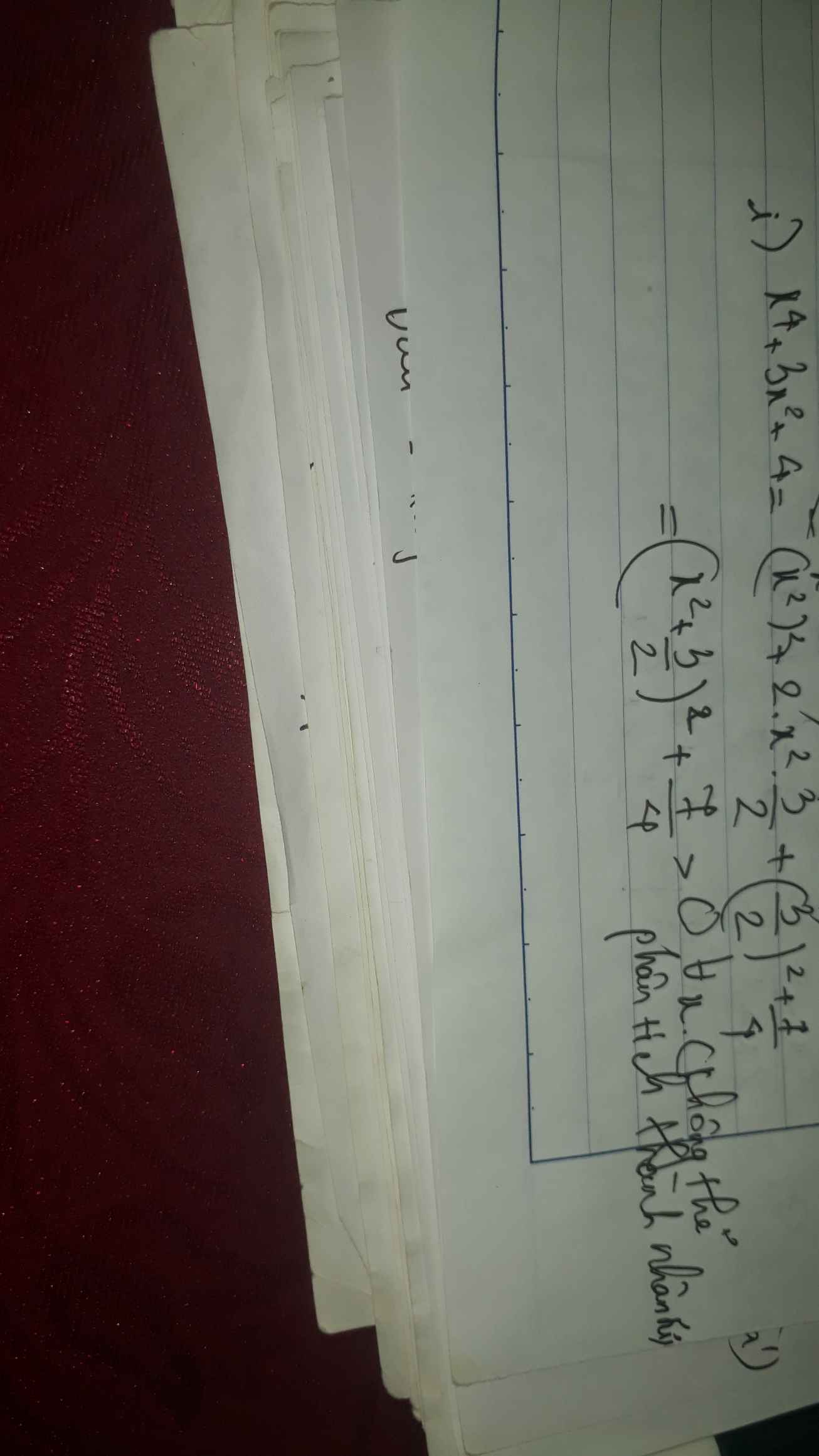
tìm số tự nhiên nhỏ nhất biết rằng khi chia cho 23 dư 21 khi chia cho 17 dư 16
a. \(x^4+3x^3-9x-9=x^3\left(x+1\right)-9\left(x+1\right)\)\(=\left(x+1\right)\left(x^3-9\right)\)