KL
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
N
2
5 tháng 1 2022
Bài 1:
\(=3x^3y-6x^2y^2+15xy\)
Bài 2:
\(=\left(x+y\right)^2-25=\left(x+y+5\right)\left(x+y-5\right)\)
5 tháng 1 2022
\(x^2+2xy-25+y^2\\ =\left(x^2+2xy+y^2\right)-5^2\\ =\left(x+y\right)^2-5^2\\ =\left(x+y-5\right)\left(x+y+5\right)\)
NN
4
4 tháng 1 2021
\(x^2-2xy+y^2-6x+6y=\left(x-y\right)^2-6\left(x-y\right)=\left(x-y\right)\left(x-y-6\right)\)
23 tháng 9 2017
a) x3-2x2-x+2
=x(x2-1)+2(-x2+1)
=x(x2-1)-2(x2-1)
=(x2-1)(x-2)
b)
x2+6x-y2+9
=x2+6x+9-y2
=(x+3)2-y2
=(x+3-y)(x+3+y)
5 tháng 1 2022
Bài 2:
a: =>4x(x+5)=0
=>x=0 hoặc x=-5
b: =>(x+3)(x-3)=0
=>x=-3 hoặc x=3
NQ
1
16 tháng 12 2022
1: =3(y^2+x^2+2xy-z^2)
=3(x+y-z)(x+y+z)
2: =2(8x^3+27y^3)
=2(2x+3y)(4x^2-6xy+9y^2)
3: =(x-y)^2-25
=(x-y-5)(x-y+5)
CM
20 tháng 10 2017
x2 + 4x – 2xy – 4y + y2 = (x2-2xy+ y2) + (4x – 4y) → bạn Việt dùng phương pháp nhóm hạng tử
= (x - y)2 + 4(x – y) → bạn Việt dùng phương pháp dùng hằng đẳng thức và đặt nhân tử chung
= (x – y)(x – y + 4) → bạn Việt dùng phương pháp đặt nhân tử chung
LP
2
MH
31 tháng 7 2015
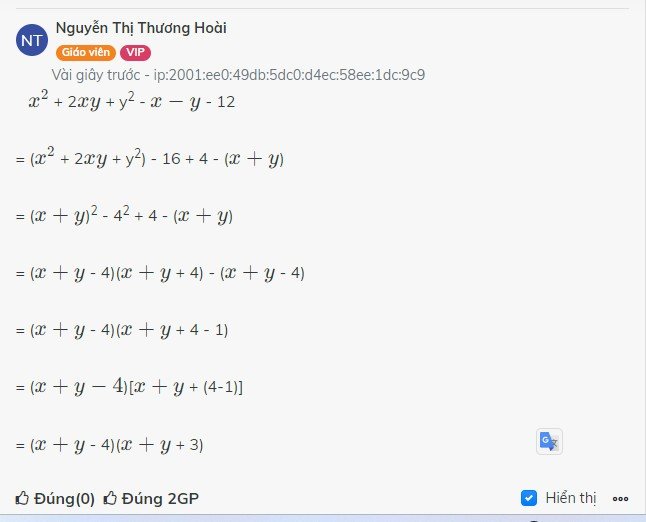
x2+2xy+y2-x-y-12
= (x+y)2-(x+y)-12
đặt x+y=z. ta có:
z2-z-12
= z2-4z+3z-12
= z(z-4)+3(z-4)
= (z-4)(z+3)
thay x+y=z:
= (x+y-4)(x+y+3)
\(x^2-25+y^2+2xy\)
\(=\left(x^2+2xy+y^2\right)-25\)
\(=\left(x+y\right)^2-5^2\)
\(=\left(x+y-5\right)\left(x+y+5\right)\)
\(x^2-25+y^2+2xy=\left(x+2\right)^2-25=\left(x+2-25\right)\left(x+2+25\right)\)
\(=\left(x-23\right)\left(x+27\right)\)
Hok tốt