Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em thứ nhất chạy nhanh hơn em thứ hai nên trong thời gian t0 = 1s em thứ nhất chạy hơn em thứ hai một đoạn đường là:
s = s1 – s2 = v1.t0 – v2.t0 = 4,8.1 – 4.1 = 0,8m.
Sau khoảng thời gian t (s), quãng đường em thứ nhất chạy hơn em thứ hai là:
S = 0,8.t
Em thứ nhất sẽ gặp em thứ hai lần đầu tiên sau thời gian t (s) khi mà quảng đường em thứ nhất chạy hơn em thứ hai trong khoảng thời gian đó bằng đúng chu vi một vòng chạy.
Khi đó ta có: S = 0,8.t = Cchu vi = 400 m
Suy ra (v1 – v2).t = 400.
Vậy thời gian ngắn nhất để hai em gặp nhau trên đường chạy là:
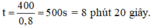

ta có:
thời gian hai xe gặp nhau là 8-7=1h
S1+S2=100
\(\Leftrightarrow v_1t_1+v_2t_2=100\)
\(\Leftrightarrow60+v_2=100\Rightarrow v_2=40\)

\(=>S1=50t\left(km\right)\) (qđ xe từ A)
\(=>S2=40t\left(km\right)\)(qđ xe từ B)
\(=>30+40t=50t=>t=3h\)
=>kể từ khi 2 xe xuất phát sau 3h thì gặp nhau
vị trí gặp nhau cách A \(Sa=S1=50.3=150km\)
Hai xe xuất phát cùng một lúc nên gọi thời gian chuyển động của hai xe là t
Gọi v1 là vận tốc của ô tô 1; v2 là vận tốc của ô tô 2
Xe đi từ A có đường đi là s1 = v1t = 40t
Hai xe chuyển động cùng chiều từ A đến B nên lúc đầu xe B cách A một đoạn s0 = 20km
Xe đi từ B cách A một đoạn đường là: s2 = s0 + v2t = 20 + 30t (km)
Khoảng cách giữa hai xe: Δs = s2 - s1 = 20 + 30t - 40t = 20 - 10t (km)

ta có:
sau 1h thì hai xe đi được:
*xe 1:30.1=30km
*xe 2:40.1=40km
khoảng cách hai xe sau 1h là:40-30+60=70km
lúc hai xe gặp nhau thì:
S1-S2=70km
\(\Leftrightarrow v_1t_1-v_2t_2=70\)
\(\Leftrightarrow60t_1-40t_2=70\)
mà t1=t2=t nên:
60t-40t=70
giải phương trình ta có:t=3.5h
a) quãng đường xe đi từ A trong 1h :S1 = v1.t = 30.1 =30km
quãng đường xe đi từ B trong 1h: S2 = v2 .t =40.1=40km
khoảng cách của 2 xe sau 1h : S' = S + S1 + S2 = 60+40-30= 70km
b) hai xe gặp nha
c) quãng đường xe đi từ A sau khi tăng tốc: S'1 = v'1.t = 50t
quãng đường xe đi từ B sau khi xe đi từ A tăng tốc: S'2 = v'1.t =40t
do 2 xe đi cùng chiều nên: S' =S'1 -S'2= 70 km
=> S'1 -S'2 = 50t -40t =70 => 10t=70 => t=7h

Tóm tắt
\(S_{AB}=60km\)
\(V_1=30km\)/\(h\)
\(V_2=40km\)/\(h\)
\(t_1=1h\)
\(t_2=1,5h\)
\(V_3=50km\)/\(h\)
_____________
a) \(S_{A'B'}=?\)
b) \(t=?;S_{BC}=?\)
Giải

a) Ta có: \(S_{A'B'}=S_{BB'}+\left(S_{AB}-S_{AA'}\right)=V_2.t_1+60-V_1.t_1=t_1\left(V_2-V_1\right)+60=40-30+60=70\left(km\right)\)
b) Gọi \(A_1\) là điểm dừng sau 1,5h đi với vận tốc 30km/h.
Ta có: \(S_{AC}=S_{AA_1}+S_{A_1C}=S_{BC}+S_{AB}\Rightarrow V_1.t_2+V_3\left(t-t_2\right)=V_2.t+60\)
\(\Rightarrow30.1,5+50\left(t-1,5\right)=40t+60\Rightarrow45+50t-75=40t+60\)
\(\Rightarrow50t-40t=75-45+60=90\Rightarrow t=9\left(h\right)\Rightarrow S_{BC}=40.9=360\left(km\right)\)
Vậy thời gian 2 điểm gặp nhau là sau 9h và cách điểm B là 360 km

a, áp dụng ct: \(2\pi R=2.3,14.\dfrac{250}{1000}=1,57km\)
\(=>S1=32,5t\left(km\right)\)
\(=>S2=35t\left(km\right)\)
\(=< pt:32,5t+1,57=35t=>t=0,628h\approx38'\)
đổi \(4h30'=270'\)
vậy lần đầu 2 xe gặp nhau lúc \(4h30'+38'\approx5h8'\)
b, \(=>\)gọi số lần gặp nhau là x (lần) \(\left(x\in N,x>0\right)\)
=>số lần gặp nhau \(x=\dfrac{1,5}{0,628}\approx2,3\)
kết hợp điều kiện \(=>x\approx2\) lần