Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Bước sóng của sóng: 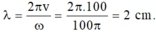
* Lưu ý rằng, khi xảy ra giao thoa sóng cơ, trên đoạn thẳng nối hai nguồn, ta có thể xem gần đúng như hiện tượng sóng dừng trên dây. Nên các cực đại liên tiếp cách nhau 0,5λ, các cực đại cùng pha thì đối xứng qua một bụng sóng (cực đại).
- Trên đoạn IM, ta xét tỉ số: 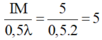
→ Hai nguồn cùng pha do đó I là cực đại, từ I đến M có 5 cực đại khác nữa, trong đó các cực đại cùng pha với I ứng với k = - 2, - 4.
- Tương tự trên đoạn IN, ta xét tỉ số: 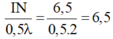
→ Trên IN có 6 cực đại, trong đó các cực đại cùng pha với I ứng với: k = +2, +4, +6.
→ Trên MN có 5 điểm cực địa và cùng pha với I.

Đáp án D
+ Bước óng cảu sóng λ = 2 πv ω = 2 π . 100 100 π = 2 cm .
Lưu ý rằng, khi xảy ra giao thoa sóng cơ, trên đoạn thẳng nối hai nguồn, ta có thể xem gần đúng như hiện tượng sóng dừng trên dây. → các cực đại liên tiếp cách nhau 0,5λ, các cực đại cùng pha thì đối xứng qua một bụng sóng (cực đại).
+ Trên đoạn IM, ta xét tỉ số: IM 0 , 5 λ = 5 0 , 5 . 2 = 5
→ Hai nguồn cùng pha do đó I là cực đại, từ I đến M có 5 cực đại khác nữa, trong đó các cực đại cùng pha với I ứng với k = –2, –4.
+ tương tự trên đoạn IN, ta xét tỉ số IN 0 , 5 λ = 6 , 5 0 , 5 . 2 = 6 , 5 .
→ Trên IN có 6 cực đại, trong đó các cực đại cùng pha với I ứng với k = +2, +4 và +6.
→ Trên MN có 5 điểm cực địa và cùng pha với I.

\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

Đáp án C
+ Điều kiện để có cực đại giao thoa với hai nguồn ngược pha
∆ d = d 2 - d 1 = ( k + 0 , 5 ) λ .
Với khoảng giá trị của ∆ d :
0 - 14 , 5 cm < ∆ d < 10 , 875 - 3 , 625 cm → - 7 , 75 ≤ k ≤ 3 , 125 .
→ Có 11 điểm dao động với biên độ cực đại.

Bước sóng \(\lambda = v/f = 1/25 = 0.04m = 4cm.\)
Độ lệch pha giữa hai nguồn sóng là \(\triangle\varphi= \varphi_2-\varphi_1 = \frac{5\pi}{6}+\frac{\pi}{6} = \pi.\)
Biên độ sóng tại điểm M là \( A_M = |2a\cos\pi(\frac{10-50}{4}-\frac{\pi}{2\pi})| =0.\)

Số điểm cực đại trên đoạn AG là số giá trị k thỏa mãn \(-AG \leq (k+\frac{\triangle \phi}{2\pi})\lambda \leq AG \Rightarrow -\frac{AB}{4}.3=10.875cm \leq (k+0.5)\lambda \leq 10.875\\ \Rightarrow -5.94 \leq k \leq 4.94 \Rightarrow k = -5,-4,\ldots,0,1,\ldots,4\)
có 10 điểm dao động cực đại trên đoạn AG

Đáp án D
*Một Hypybol cực đại sẽ cắt AB tại hai điểm đường thẳng CD tại 2 điểm (trừ trường hợp hypybol cắt C tại 1 điểm). Vì trên d có 13 điểm dao động với biên độ cực đại và 
nên C là điểm thuộc cực đại bậc xa trung tâm nhất sẽ thuộc cực đại bậc 7.
Do đó ta có ![]()
Tốc độ truyền sóng là ![]()



\(\lambda=\frac{v}{f}=\frac{1}{50}=0,2m\)
Phương trình sóng tại I là :
\(u_I=u_{I\left(A\right)}+u_{I\left(B\right)}=\left(a+b\right)\cos\left(100\pi t-\frac{AB}{2}\pi\right)\)
Lấy C thuộc MN thỏa mãn: IC = d theo thứ tự ICB với IC = d.
\(u_C=u_{C\left(A\right)}+u_{C\left(B\right)}=a\cos\left(100\pi t-\pi\left(d+\frac{AB}{2}\right)\right)+b\cos\left(100\pi t-\pi\left(\frac{AB}{2}-d\right)\right)\)
Do uC có biên độ cực đại là a+b và cùng pha với I nên u_C(A) cùng pha với u_C(B). Khi đó
\(\pi d=k2\pi\Rightarrow-5\le2k\le6,5\Rightarrow k=-2,1,0,1,2,3\)
Trong đó có cả I vậy cón 5 điểm nữa dao động cùng pha với I.
Đáp án C.