Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tự vẽ hình nha=0
Ta có:
\(AC=\sqrt{\left(\dfrac{1}{2}CD\right)^2+\left(\dfrac{1}{2}AB\right)^2}=\sqrt{6^2+12^2}=6\sqrt{5}\left(cm\right)\)
\(R=\dfrac{OO'}{2}+\dfrac{CD}{2}\)
Mặt khác tứ giác `AOBO'` là hình thoi:
\(2R=OO'+CD=OO'+12\left(cm\right)\\ \Rightarrow R=10\left(cm\right)\)
`HaNa♫D`

H la giao diem cua AB va CD ta co AH = BH =1/2 AB =12cm
cH=DH=6cm
=> AC=AD =\(\sqrt{12^2+6^2}\)=\(6\sqrt{5}\)......................

ta có: ON = 8 = OM + MN => OM = ON - MN
và: O'M = 6 = O'N + MN => O'N = O'M - MN
mà: O'O = OM + MN + NO' = 11
=> O'O= ON - MN + MN + O'M - MN
= ON + O'M - MN
Thay vào, ta được: 11= 8+ 6 - MN => MN =3
Vậy MN = 3 cm
11 =

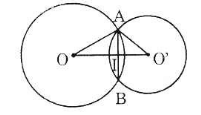
- Trường hợp 1: O và O' nằm khác phía đối với AB
Gọi I là giao điểm của OO' và AB. Theo tính chất đường nối tâm ta có
\(AB\perp OO'\) ; AI = IB = 12
Áp dụng định lí Pitago , ta được :
\(OI=\sqrt{OA^2-AI^2}=\sqrt{20^2-12^2}=\sqrt{256}=16\left(cm\right)\)
\(IO'=\sqrt{O'A^2-AI^2}=\sqrt{15^2-12^2}=\sqrt{81}=9\left(cm\right)\)
Vậy OO' = OI + IO' = 16 + 9 = 25 ( cm )
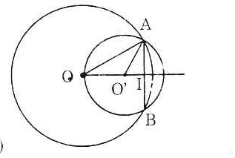
- Trường hợp 2: O và O' nằm cùng phía đối với AB
Như TH1 , ta lại có :
\(OI=\sqrt{OA^2-AI^2}=16\left(cm\right)\)
\(O'I=\sqrt{O'A^2-AI^2}=9\left(cm\right)\)
Vậy OO' = OI – O'I = 16 – 9 = 7 ( cm )

a) Trường hợp O và O’ nằm khác phía đối với AB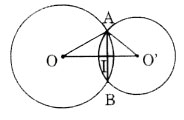
Ta có: AI =1/2 AB = 12
OI2 = OA2 – AI2
=400-144 =256
⇒ OI =16
O’I2 = O’A2 – AI2 =255 -144 =81
⇒ O’I = 9
Ta có: OO’ = OI + OI’ = 16 + 9 =25 (cm).
b) Trường hợp O và O’ nằm cùng phía đối với AB.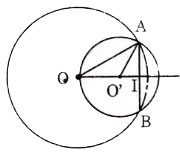
Ta có: OI2 = OA2 – AI2 = 256
⇒ OI =16
Tương tự O’I= 9
Do đó: OO’= OI – O’I =16 – 9= 7(cm)

Hình tự vẽ ạ!
a, Xét \(\Delta MED\)và \(\Delta AEM\)có:
\(\widehat{DME}=\widehat{ACM}\left(so-le-trong\right)\)
\(\widehat{MAE}=\widehat{ACM}\)(cùng chắn cung \(AD\))
\(\Rightarrow\widehat{DME}=\widehat{MAE}\)
\(\widehat{E}\)là góc chung.
\(\Rightarrow\Delta MED~\Delta AEM\left(1\right)\)
Xét \(\Delta BED\)và \(\Delta AEB\)có:
\(\widehat{EBD}=\widehat{BAD}\)(cùng chắn cung \(BD\))
\(\widehat{E}\)là góc chung
\(\Rightarrow\Delta BED~\Delta AEB\left(3\right)\)
b, Từ \(\left(1\right)\Rightarrow\frac{ME}{AE}=\frac{ED}{EM}\Rightarrow ME^2=ED.EA\left(2\right)\)
Từ \(\left(3\right)\Rightarrow\frac{EB}{EA}=\frac{ED}{EB}\Rightarrow EB^2=EA.ED\left(4\right)\)
Từ \(\left(2\right)\left(4\right)\Rightarrow EM=EB\)
\(\Rightarrow E\)là trung điểm của \(MB\left(Đpcm\right)\)
~~~Happy new year ~~~