
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Hướng dẫn:
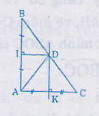
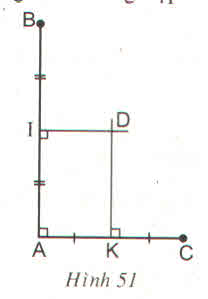
Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=> ˆADK=ˆCDKADK^=CDK^
hay DK là phân giác ˆADCADC^
=> ˆADKADK^ = 1212ˆADCADC^
∆ADI = ∆BDI (c.c.c)
=> ˆADI=ˆBDIADI^=BDI^
=> DI là phân giác ˆADBADB^
=> ˆADIADI^ = 1212 ˆADBADB^
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay ˆADKADK^ + ˆADIADI^ = 900
Do đó 1212ˆADCADC^ + 1212 ˆADBADB^ = 900
=> ˆADCADC^ + ˆADBADB^ = 1800

Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=> ˆADK=ˆCDKADK^=CDK^
hay DK là phân giác ˆADCADC^
=> ˆADKADK^ = 1212ˆADCADC^
∆ADI = ∆BDI (c.c.c)
=> ˆADI=ˆBDIADI^=BDI^
=> DI là phân giác ˆADBADB^
=> ˆADIADI^ = 1212 ˆADBADB^
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay ˆADKADK^ + ˆADIADI^ = 900
Do đó 1212ˆADCADC^ + 1212 ˆADBADB^ = 900
=> ˆADCADC^ + ˆADBADB^ = 1800

Hướng dẫn:
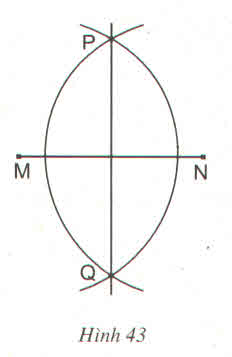
Ta có: Hai cung tròn tâm M và N có bán kính bằng nhau
Nên MP = NP và MQ = NQ => P; Q cách đều hai mút M, N của đoạn thẳng MN nên P; Q thuộc đường trung trực của MN hay đường thẳng qua P, Q là đường trung trực của MN
Hướng dẫn:

Ta có: Hai cung tròn tâm M và N có bán kính bằng nhau
Nên MP = NP và MQ = NQ => P; Q cách đều hai mút M, N của đoạn thẳng MN nên P; Q thuộc đường trung trực của MN hay đường thẳng qua P, Q là đường trung trực của MN

Ghép a-d' ; b –a', c-b', d-c'
Trong một tam giác
a - d' đường phân giác xuất phát từ đỉnh A - là đoạn thẳng có hai mút là đỉnh A và giao điểm của cạnh BC với tia phân giác của góc A.
b - a' đường trung trực ứng với cạnh BC - là đường vuông góc với cạnh BC tại trung điểm của nó.
c - b' đường cao xuất phát từ đỉnh A - là đoạn vuông góc kẻ từ A đến đường thẳng BC.
d - c' đường trung tuyến xuất phát từ đỉnh A - là đoạn thẳng nối A với trung điểm của cạnh BC.
Trả lời
Ghép a-d' ; b –a', c-b', d-c'
Trong một tam giác
a - d' đường phân giác xuất phát từ đỉnh A - là đoạn thẳng có hai mút là đỉnh A và giao điểm của cạnh BC với tia phân giác của góc A.
b - a' đường trung trực ứng với cạnh BC - là đường vuông góc với cạnh BC tại trung điểm của nó.
c - b' đường cao xuất phát từ đỉnh A - là đoạn vuông góc kẻ từ A đến đường thẳng BC.
d - c' đường trung tuyến xuất phát từ đỉnh A - là đoạn thẳng nối A với trung điểm của cạnh BC.

\(\left(x-3\right).\left(x-2015\right)< 0\)
\(\Rightarrow\left(x-3\right)và\left(x-2015\right)\) phải khác dấu
\(\Rightarrow\left(x-3\right)< \left(x-2015\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x-3>0\\x-2015< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>3\\x< 2015\end{matrix}\right.\)
\(\Rightarrow3< x< 2015\)
\(\Rightarrow x\in\left\{4;5;6;7;8;...;2013;2014\right\}\)
( ko bt đúng hay sai nx )
thám tử
\(\left(x-3\right)\left(x-2015\right)< 0\)
Với mọi \(x\in R\) thì:
\(x-2015< x-3\)
Khi đó: \(\left\{{}\begin{matrix}x-2015< 0\\x-3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 2015\\x>3\end{matrix}\right.\)
Nên \(3< x< 2015\)

Ghép a-b', b-a', c-d', d-c'
Trong một tam giác
a - b' trọng tâm - là điểm chung của ba đường trung tuyến
b - a' trực tâm - là điểm chung của ba đường cao
c - d' điểm (nằm trong tam giác) cách đều ba cạnh - là điểm chung của ba đường phân giác
d - c' điểm cách đều ba đỉnh - là điểm chung của ba đường trung trực
Trả lời
Ghép a-b', b-a', c-d', d-c'
Trong một tam giác
a - b' trọng tâm - là điểm chung của ba đường trung tuyến
b - a' trực tâm - là điểm chung của ba đường cao
c - d' điểm (nằm trong tam giác) cách đều ba cạnh - là điểm chung của ba đường phân giác
d - c' điểm cách đều ba đỉnh - là điểm chung của ba đường trung trực
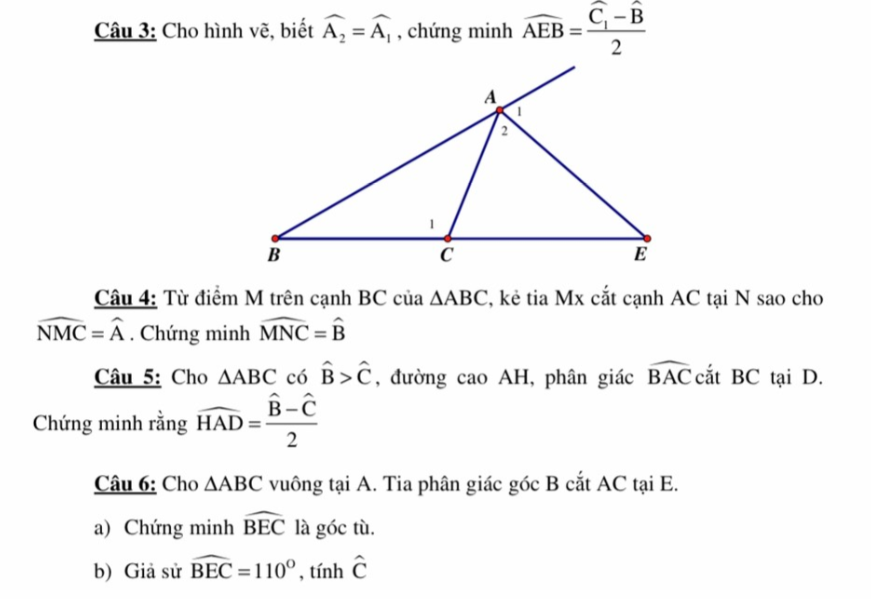
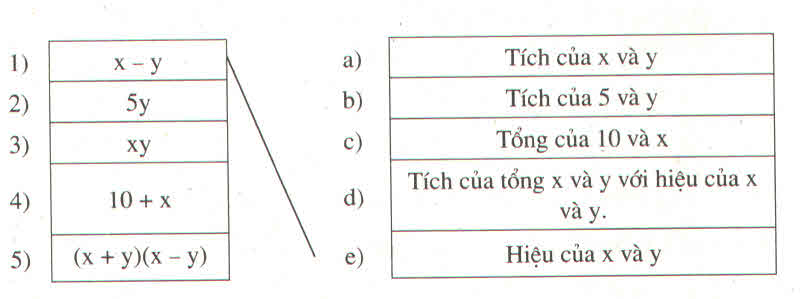
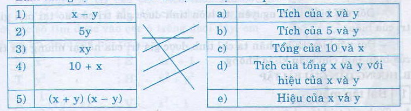












Câu 3:
Theo tính chất góc ngoài:
\(\widehat{AEB}=\widehat{C_1}-\widehat{A_2}=\widehat{C_1}-\widehat{A_1}=\widehat{C_1}-\widehat{B}-\widehat{AEB}\\ \Rightarrow2\widehat{AEB}=\widehat{C_1}-\widehat{B}\\ \Rightarrow\widehat{AEB}=\dfrac{\widehat{C_1}-\widehat{B}}{2}\)
cho em hỏi là tính chất góc ngoài còn có cả trừ ạ??
* AEB= C1- A2