
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Để $M$ có giá trị lớn nhất thì $a-8$ phải là số tự nhiên khác 0 nhỏ nhất
Suy ra $a-8=1$
$a=8+1=9$
Khi đó $M$ nhận giá trị lớn nhất là: $87,5:1=87,5$

diện tích tôn để là cái thùng là:
( 60 + 40 ) x 2 x 80 + 60 x 40 = 18400 ( dm2 )
đáp số: 18400 dm2.

Diện tích tam giác ABC là: 3 x 4 : 2 = 6 (dm2)
Đáp số:...
Diện tích tam giác ABC là:
\(3\times4:2=6\left(dm^2\right)\)
Đáp số: \(6\left(dm^2\right)\)

đổi 2 ngày 8 giờ = 56 giờ
3 ngày 9 giờ = 81 giờ
1 giờ làm được số sản phẩm là:
112 : 56 = 2 ( sản phẩm )
làm trong 3 ngày 9 giờ thì được số sản phẩm là:
2 x 81 = 162 ( sản phẩm )
đáp số 162 sản phẩm
1gio lam duoc so san pham la
8chia112bangbao nhieu
lam 3ngay 9 gio duoc so san pham la
lay 9 nhan cho 1gio
dshet

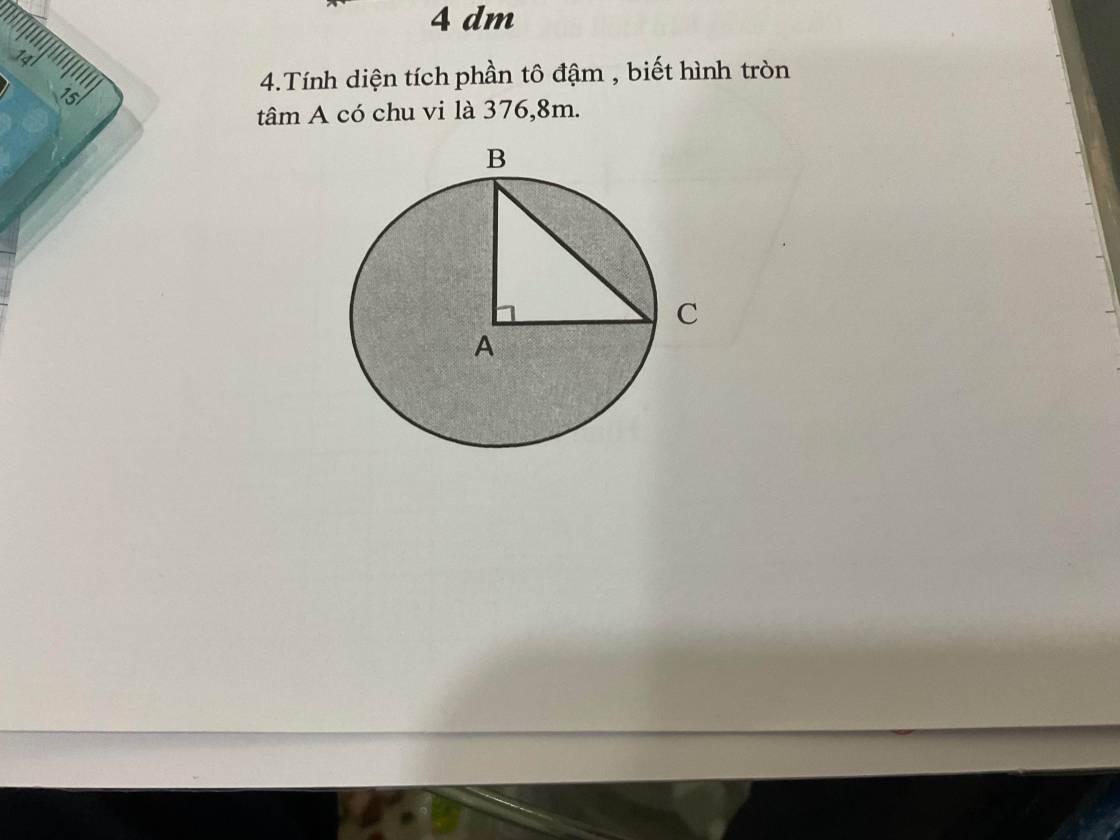
Bán kính hình tròn tâm A là:
\(376,8:3,14:2=60\left(m\right)\)
Diện tích tam giác ABC là:
\(60\times60:2=1800\left(m^2\right)\)
Diện tích hình tròn là:
\(60\times60\times3,14=11304\left(m^2\right)\)
Diện tích phần tô đậm là:
\(11304-1800=9504\left(m^2\right)\)

Lời giải:
Diện tích phần hình thang của mảnh vườn:
$(40+40+10)\times 20:2=900$ (m2)
Diện tích phần tam giác của mảnh vườn:
$20\times 40:2=400$ (m2)
Diện tích mảnh vườn: $900+400=1300$ (m2)
Đáp án A.


Lời giải:
a.
AH là chiều cao của các tam giác: $ABM, ABH, AMH, ABC, AMC, AHC$
b. $BM=BC:3 = 18:3=6$ (dm)
$S_{ABM}=\frac{AH\times BM}{2}=\frac{4,5\times 6}{2}=13,5$ (dm2)

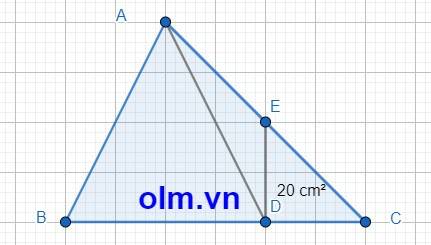
SCDE = \(\dfrac{1}{2}\)SADC (vì hai tam gác có chung đường cao hạ từ đỉnh D xuống đáy AC và CE = \(\dfrac{1}{2}\)AC)
⇒ SADC = 20 : \(\dfrac{1}{2}\) = 40 (cm2)
BC = DC + BD = DC + 2 x DC = 3 x DC
SABC = 3 x SADC (vì có chung chiều cao hạ từ đỉnh A xuống đáy BC và BC = 3 x DC)
SABC = 40 x 3 = 120 (cm2)
ĐS...







Bài 2:
1.
$=(\frac{1}{7}+\frac{2}{7}+\frac{4}{7})+(\frac{3}{11}+\frac{8}{11})+2010$
$=\frac{7}{7}+\frac{11}{11}+2010=1+1+2010=2012$
2.
$=(\frac{2}{3}-\frac{2}{3})+(\frac{-3}{4}+\frac{3}{4})+(\frac{4}{5}-\frac{4}{5})+(\frac{-5}{6}+\frac{5}{6})+(\frac{6}{7}-\frac{6}{7})+(\frac{-7}{8}+\frac{7}{8})+\frac{1}{2012}$
$=0+0+0+0+0+0+\frac{1}{2012}=\frac{1}{2012}$
3.
$=\frac{1}{5-4}{4.5}+\frac{6-5}{5.6}+\frac{7-6}{6.7}+...+\frac{1}{20-19}{19.20}$
$=\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+..+\frac{1}{19}-\frac{1}{20}$
$=\frac{1}{4}-\frac{1}{20}=\frac{1}{5}$
4.
\(=182\left[\frac{1+\frac{1}{5}-\frac{2}{7}+\frac{5}{13}}{2(1+\frac{1}{5}-\frac{2}{7}+\frac{5}{13})}: \frac{4(1-\frac{1}{33}-\frac{1}{57}+\frac{1}{7000})}{1-\frac{1}{33}-\frac{1}{57}+\frac{1}{7000}}\right]:\frac{10101\times 91}{10101\times 80}\)
$=182(\frac{1}{2}:4):\frac{91}{80}=182\times \frac{1}{8}\times \frac{80}{91}$
$=\frac{91\times 2\times 80}{8\times 91}=\frac{160}{8}=20$