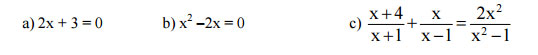K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AP
0
QD
5 tháng 7 2016
a) 2x + 3 = 0 → x = -3/2. Vậy tập nghiệm của pt la S = {-3/2}.
b) x² – 2x = 0 ↔ x(x – 2) = 0 ↔ x = 0 hoặc x = 2 Vậy tập nghiệm của pt là S = {0; 2}.
c) ĐKXĐ: x ≠ 1; x ≠ -1
Quy đồng hai vế và khử mẫu, ta có:
Suy ra: x² + 3x – 4 + x² + x = 2x² ↔ 4x = 4 ↔ x = 1 (không thỏa mãn điều kiện). Vậy phương trình đã cho vô nghiệm.
ND
7 tháng 2 2017
ai giải hộ bài này vs
giải phương trình: (2x -5)^3-(3x-4)^3+(x+1)^3=0 lớp 8
DH
1
12 tháng 7 2016
a) 10 – 4x = 2x – 3
<=> – 4x – 2x = – 3 – 10
<=> – 6x = -13
<=> x = \(\frac{13}{6}\)
Vậy tập nghiệm S = {\(\frac{13}{6}\) }
Điều kiện: x ≠ \(\frac{3}{2}\) ; x ≠ 0
=> x – 3 = 5(2x – 3)
<=> x – 3 = 10x – 15
<=> x – 10x = – 15 + 3
<=> x – 10x = – 15 + 3
<=> x = \(\frac{4}{3}\) ( TMĐK)
Vậy tập nghiệm của phương trình là: S = { \(\frac{4}{3}\) }
c) | 2x – 1| = 3 (1)
Ta có | 2x – 1| = 2x – 1 khi 2x – 1 ≥ 0 hay x ≥ \(\frac{1}{2}\)
| 2x – 1| = – (2x – 1) khi 2x – 1 < 0 hay x <\(\frac{1}{2}\)
Vậy để giải phương trình (1), ta quy về giải hai phương trình sau:
* Phương trình 2x – 1 = 3 với điều kiện x ≥ \(\frac{1}{2}\)
Ta có 2x – 1 = 3
<=> 2x = 3 + 1
<=> x = 2 (TMĐK)
* Phương trình – (2x – 1) = 3 với điều kiện x <\(\frac{1}{2}\)
Ta có – 2x + 1 = 3
<=> – 2x = 3 – 1
<=> x = -1 (TMĐK)
Vậy tập nghiệm của phương trình là : S = { – 1; 2 }