Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi số cây của đội \(1;2;3\) đã trồng lần lược là \(a;b;c\) \(\left(0< a;b;c\in Z\right)\)
vì \(\dfrac{1}{2}\) số cây của đội \(1\) trồng bằng \(\dfrac{2}{3}\) số cây của đội \(2\) và bằng \(\dfrac{3}{4}\) số cây của đội \(3\)
\(\Rightarrow\dfrac{1}{2}a=\dfrac{2}{3}b=\dfrac{3}{4}c\) (1)
vì số cây của đội \(2\) trồng ít hơn tổng số cây của đội \(1\) và \(3\) là \(55\) cây
\(\Rightarrow b+55=a+c\) (2)
từ (1) và (2) ta có : \(\left\{{}\begin{matrix}a=60\\b=45\\c=40\end{matrix}\right.\left(tm\right)\)
vậy ..............................................................................................................................
Gọi a,b,c lần lượt là số cây của 3 đội 1,2,3 Theo đề ta có: 1/2a=2/3b=3/4c (1) và a+c-b=55 Ta lấy (1) chia cho BCNN(1,2,3)=6, ta được như sau: a/12=b/9=c/8 và a+c-b=55 Áp dụng t/c tỉ số bằng nhau, ta có a/12=b/9=c/8=a+c-b/12+8-9=55/11=5 Suy ra a=12.5=60; b=9.5=45; c=8.5=40

Gọi phương trình đường thẳng \(d:ax + by + c = 0\)
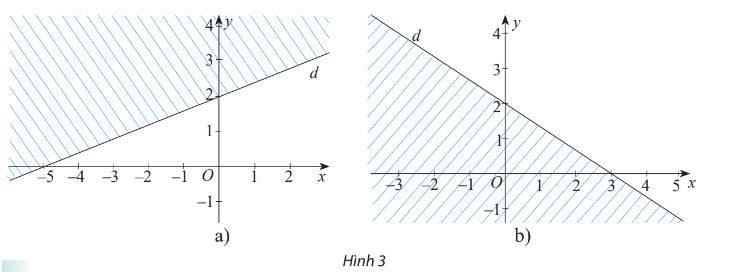
a) Từ hình a) ta thấy d đi qua hai điểm\(A(0;2)\) và \(B( - 5;0)\)
\( \Rightarrow \left\{ \begin{array}{l}b.2 + c = 0\\ - 5a + c = 0\end{array} \right. \Rightarrow c = 5a = - 2b\)
Chọn \(a = 2 \Rightarrow b = - 5;c = 10\) và \(d:2x - 5y + 10 = 0\)
Điểm O (0;0) thuộc miền nghiệm và \(2.0 - 5.0 + 10 = 10 > 0\)
Vậy bất phương trình cần tìm là \(2x - 5y + 10 > 0\)
b) Từ hình b) ta thấy d đi qua hai điểm\(A(0;2)\) và \(B(3;0)\)
\( \Rightarrow \left\{ \begin{array}{l}2b + c = 0\\3a + c = 0\end{array} \right. \Rightarrow - c = 3a = 2b\)
Chọn \(a = 2 \Rightarrow b = 3;c = - 6\) và \(d:2x + 3y - 6 = 0\)
Điểm O (0;0) không thuộc miền nghiệm và \(2.0 + 3.0 - 6 = - 6 < 0\)
Vậy bất phương trình cần tìm là \(2x + 3y - 6 > 0\)

Tham khảo:
Để pha x lít nước cam loại I cần 30x g bột cam,
Để pha y lít nước cam loại II cần 20y g bột cam,
Vì Cúc chỉ có thể dùng không quá 100 gam bột cam nên ta có bất phương trình \(30x + 20y \le 100\)
\( \Leftrightarrow 3x + 2y - 10 \le 0\)
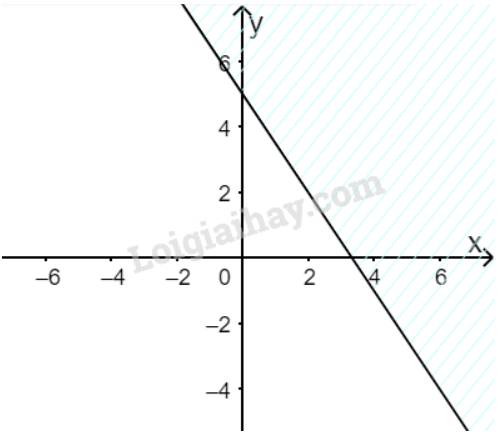
Vẽ đường thẳng \(\Delta :3x + 2y - 10 = 0\) đi qua hai điểm \(A(0;5)\) và \(B\left( {2;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(3.0 + 2.0 - 10 = - 10 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)

Đáp án: A
II sai vì trong trường hợp B ⊂ A thì A ∪ B = A nên |A ∪ B| = |A|. Do đó |A| ≤ |A ∪ B|.
III sai vì trong trường hợp trong số các phần tử của B không có phần tử nào thuộc A thì A \ B = A nên |A ∪ B| = |A|. Do đó |A \ B| ≤ |A ∪ B|.

Ta có : \(\overline{A}=\overline{A_1UA_2UA_3}=\overline{A_1}\) \(\overline{A_2}\)\(\overline{A_3}\)= sự kiện không có ai bắn trúng
\(\Rightarrow P\left(\overline{A}\right)=\)\((\overline{A_1}\)\(\overline{A_2}\)\(\overline{A_3})\)\(=P\left(\overline{A_1}\right)P\left(\overline{A_2}\right)P\left(\overline{A_3}\right)=0,5.0,4.0,3=0,06\)
\(\Rightarrow P\left(A\right)=1-P\left(\overline{A}\right)=1-0,06=0,94\)
Vậy xác xuất để con thú bị bắn trúng là 0,94

Đáp án: A
A ∩ B = ∅ => Các phần tử thuộc A thì không thuộc B nên số phần tử của bằng tổng số phần tử của A và B.
=> I đúng.
II và III sai vì khi ±|A ∩ B| = ∅ làm thay đổi tổng số phần tử của A và B.

À, nghĩa là các dữ liệu "ném trúng I và II" nghĩa là chỉ trúng I và II, còn III chắc chắn ko trúng, tương tự với 2 cái còn lại đúng ko?
Phạm Hoàng Lê Nguyên SR ông anh vì ko làm đc nên chỉ có câu: Chúc may mắn!!!!!!!!!!!!!!!!!!!