Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II sản xuất ra.
Như vậy tiền lãi có được là L = 3x + 5y (nghìn đồng).
Theo đề bài: Nhóm A cần 2x + 2y máy;
Nhóm B cần 0x + 2y máy;
Nhóm C cần 2x + 4y máy;
Vì số máy tối đa ở nhóm A là 10 máy, nhóm B là 4 máy, nhóm C là 12 máy nên x, y phải thỏa mãn hệ bất phương trình: 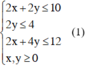
Khi đó bài toán trở thành: trong các nghiệm của hệ bất phương trình (1) thì nghiệm (x = xo; y = yo) nào cho L = 3x + 5y lớn nhất.
Miền nghiệm của hệ bất phương trình (1) là ngũ giác ABCDE kể cả miền trong.
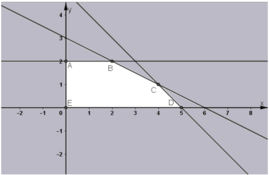
Ta có: L đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác ABCDE.
Tính giá trị của biểu thức L = 3x + 5y tại các đỉnh ta được:
Tại đỉnh A(0;2), L = 10
Tại đỉnh B(2; 2), L = 16
Tại đỉnh C(4; 1), L = 17
Tại đỉnh D(5; 0), L = 15
Tại đỉnh E(0; 0), L = 0.
Do đó, L = 3x + 5y lớn nhất là 17 (nghìn đồng) khi: x = 4; y = 1
Vậy để có tiền lãi cao nhất, cần sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm loại II.

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II được nhà máy lập kế hoạch sản xuất. Khi đó số lãi nhà máy nhân được là P = 3x + 5y (nghìn đồng).
Các đại lượng x, y phải thỏa mãn các điều kiện sau:
(I)
(II)
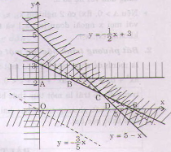
Miền nghiệm của hệ bất phương trình (II) là đa giác OABCD (kể cả biên).
Biểu thức F = 3x + 5y đạt giá trị lớn nhất khi (x; y) là tọa độ đỉnh C.
(Từ 3x + 5y = 0 => y = Các đường thẳng qua các đỉnh của OABCD và song song với đường y =
cát Oy tại điểm có tung độ lớn nhất là đường thẳng qua đỉnh C).
Phương trình hoành độ điểm C: 5 - x = <=> x = 4.
Suy ra tung độ điểm C là yc = 5 - 4 = 1. Tọa độ C(4; 1). Vậy trong các điều kiện cho phép của nhà máy, nếu sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm đơn vị loại II thì tổng số tiền lãi lớn nhất bằng:
Fc = 3.4 + 5.1 = 17 nghìn đồng.

a) Số cách chọn 1 bạn từ nhóm 15 bạn là tổ hợp chập 1 của 15 \(C_{15}^1 = 15\) cách
b) Việc chọn 3 thành viên của nhóm đang học ở ba lớp khác nhau gồm 3 công đoạn:
Công đoạn 1: Chọn 1 bạn từ lớp 10A có 4 cách
Công đoạn 2: Chọn 1 bạn từ lớp 10B có 5 cách
Công đoạn 3: Chọn 1 bạn từ lớp 10C có 6 cách
Áp dụng quy tắc nhân, ta có \(4.5.6 = 120\) cách chọn 3 thành viên của nhóm đang học ở ba lớp khác nhau
c) Việc chọn 2 thành viên của nhóm đang học ở hai lớp khác nhau có 3 trường hợp:
TH1: 2 bạn đang học ở lớp 10A và 10B có \(4.5 = 20\) cách
TH2: 2 bạn đang học ở lớp 10A và 10C có \(4.6 = 24\) cách
TH3: 2 bạn đang học ở lớp 10C và 10B có \(6.5 = 30\) cách
Áp dụng quy tắc cộng, ta có \(20 + 24 + 30 = 74\) cách chọn 2 thành viên của nhóm đang học ở hai lớp khác nhau

Gọi số công nhân ban đầu của tổ đó là x(x>2 x\(\in\)N)
Năng suất mỗi người phải làm theo dự định là: \(\frac{540}{x}\)(sản phẩm)
Do có 2 công nhân phải đi làm việc khác nên số người còn lại là: x-2 (người)
Năng suất thực tế mỗi công nhân phải làm là: \(\frac{540}{x-2}\)(sản phẩm)
Vì thực tế mỗi người phải làm thêm 3 sản phẩm nên ta có phương trình:
\(\frac{540}{x-2}\)-\(\frac{540}{x}\)=3
<=> 540x-540(x-2)=3.x(x-2)
<=> 540x -540x+1080=3\(x^2\)-6x
<=> 3\(x^2\)-6x-1080=0
<=> \(\left[\begin{array}{nghiempt}x=20\\x=-18\left(loại\right)\end{array}\right.\)
vậy ban đầu có 20 công nhân

Việc phân công các bạn tình nguyện làm các việc trên gồm 3 công đoạn
Công đoạn 1: Chọn 3 bạn để hỗ trợ đi lại, mỗi cách chọn 3 bạn từ nhóm 7 bạn để làm công việc này là một tổ hợp chập 3 của 7 phần tử. Do đó, số cách chọn 3 bạn làm công việc hỗ trợ đi lại là: \(C_7^3 = \frac{{7!}}{{3!.4!}} = 35\) (cách)
Công đoạn 2: Chọn 2 bạn để hỗ trợ tắm rửa, mỗi cách chọn 2 bạn từ nhóm 4 bạn còn lại để làm công việc này là một tổ hợp chập 2 của 4 phần tử. Do đó, số cách chọn 2 bạn làm công việc hỗ trợ tắm rửa là: \(C_4^2 = \frac{{4!}}{{2!.2!}} = 6\) (cách)
Công đoạn 3: Chọn 2 bạn để hỗ trợ ăn uống từ 2 bạn cuối cùng, có 1 cách duy nhất
Áp dụng quy tắc nhân, ta có số cách phân công các bạn trong nhóm làm công việc trên là \(35.6.1 = 210\) (cách)

Tổng số tiền 2 lần lĩnh là:
480 000 + 540 000 = 1020 000 (đồng)
a) Nếu nhóm đó có 3 người thì trung bình mỗi người làm được:
1020 000 : 3 = 340 000 (đồng)
b) Nếu nhóm đó có 4 người thì trung bình mỗi người làm được:
1020 000 : 4 = 255 000 (đồng)

a)
Do x là số lượng khách thứ 51 trở lên nên x>0.
Cứ thêm 1 người thì giá còn (300000-5 000.1) đồng/người cho toàn bộ hành khách.
Thêm x người thì giá còn (300 000-5 000.x) đồng/người cho toàn bộ hành khách.
Doanh thu theo x: \(\left( {50 + x} \right).\left( {300000 - 5000x} \right)\) (VNĐ)
b) Do chi phí thực sự cho chuyến đi là 15 080 000 đồng nên để công ty không bị lỗ thì doanh thu phải lớn hơn hoặc bằng 15 080 000 đồng
Khi đó:
\(\begin{array}{l}\left( {50 + x} \right).\left( {300000 - 5000x} \right) \ge 15080000\\ \Leftrightarrow \left( {50 + x} \right).5000.\left( {60 - x} \right) \ge 15080000\\ \Leftrightarrow \left( {x + 50} \right)\left( {60 - x} \right) \ge 3016\\ \Leftrightarrow - {x^2} + 10x + 3000 \ge 3016\\ \Leftrightarrow - {x^2} + 10x - 16 \ge 0\\ \Leftrightarrow {x^2} - 10x + 16 \le 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {x - 8} \right) \le 0\\ \Leftrightarrow 2 \le x \le 8\end{array}\)
Vậy số người của nhóm du khách nhiều nhất là 58 người.


Cảm ơn bạn nha