K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QN
1
FI
2
12 tháng 12 2021
Các bất đẳng thức nổi tiếng
- Bất đẳng thức Bunyakovsky.
- Bất đẳng thức Azuma.
- Bất đẳng thức Bernoulli.
- Bất đẳng thức Boole.
- Bất đẳng thức Cauchy-Schwarz.
- Bất đẳng thức cộng Chebyshev.
- Bất đẳng thức Chernoff.
- Bất đẳng thức Cramer-Rao
- :333
SS
12 tháng 12 2021
Tôi đã học :
-bất đảng thức cô-si
-bất đảng thức bunyakovsky
về phần ví dụ thì tui chịu nha
Quên hết rùi
CM
17 tháng 5 2017
- Trong mặt phẳng (P) cho hai đường thẳng Δ và l song song với nhau, cách nhau một khoảng bằng r. Khi quay mặt phẳng (P) xung quanh trục Δ thì đường thẳng l sinh ra một mặt tròn xoay gọi là mặt trụ tròn xoay và được gọi tắt là mặt trụ.
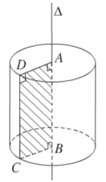
- Hình trụ là hình giới bạn bởi mặt trụ và hai đường tròn bằng nhau, là giao tuyến của mặt trụ và 2 mặt phẳng vuông góc với trục.
Hình trụ là hình tròn xoay khi sinh bởi bốn cạnh của hình một hình chữ nhật khi quay xung quanh một đường trung bình của hình chữ nhật đó.
- Khi quay một tam giác vuông góc AOC một vòng quanh cạnh góc vuông OA cố định thì được một hình nón.
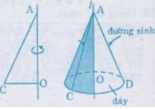
+ Cạnh OC tạo nên đáy của hình nón, là một hình nón tâm O.
+ Cạnh AC quét lên mặt xung quanh của hình nón, mỗi vị trí của nó được gọi là một đường sinh, chẳng hạn AD là một đường sinh .
+ A là đỉnh và AO là đường cao của hình nón.
KA
1
CT
10 tháng 11 2021
Tham khảo :
Nhị thức Newton là 1 công thức khai triển hàm mũ của tổng. Cụ thể là khai triển một nhị thức bậc n ((a+b)n) thành một đa thức có n+1 số hạng.
HT
Công thức
2 tháng 7 2019
Lời giải chi tiết
Ví dụ hàm số y = x4
Có đạo hàm y’ = 4x3
Cho y’ = 0 thì x = 0.
học tốt
SG
1
15 tháng 5 2022
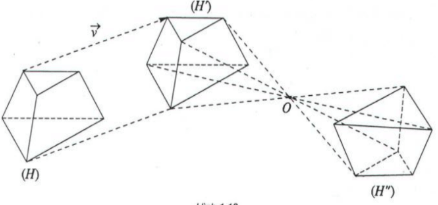
Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến đa diện này thành đa diện kia.
Ví dụ về đa diện bằng nhau:
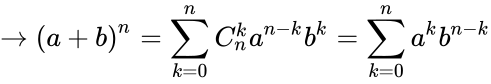
40^0