Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là số câu hỏi được trả lời đúng ở vòng sơ tuyển (x nguyên dương)
Số câu hỏi trả lời sai: 10 – x
Số điểm người dự thi đạt được: 10 + 5x – (10 -x)
Người dự thi muốn thi tiếp vòng sau thì 10 + 5x – (10 -x) ≥ 40
⇔ 6x ≥ 40 ⇔ x ≥ 20/3. Do x nguyên dương nên x ∈ {7;8;9;10}

Gọi x là số câu trả lời đúng (0 ≤ x ≤ 10, x ∈ N)
Số câu trả lời sai: 10 – x
Trả lời đúng x câu được 5x (điểm), trả lời sai 10 –x (câu) bị trừ (10- x) điểm.
Do đó, sau khi trả lời 10 câu thì người dự thi sẽ có: 5x – (10 – x) + 10
Để được dự thi tiếp vòng sau thì
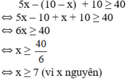
Vậy người dự thi phải trả lời chính xác ít nhất 7 câu hỏi thì mới được dự thi ở vòng sau.

Gọi x là số câu trả lời đúng
Số câu trả lời sai: 10 – x
Sau khi trả lời 10 câu thì người dự thi sẽ có: 5x – (10 – x) + 10
Để được dự thi tiếp vòng sau thì
5x – (10 – x ) +10 ≥ 40
⇔ 5x - 10 + x + 10 ≥ 40
⇔6x ≥ 40
⇔ x ≥\(\dfrac{20}{3}\) Vì x là số nguyên dương nhỏ hơn hay bằng 10 nên 203≤x≤10203≤x≤10
Vậy người dự thi phải trả lời chính xác ít nhất 7 câu hỏi thì mới được dự thi tiếp ở vòng sau.

- Số các số chia hết cho 8 trong dãy trên là: \(\dfrac{2016-8}{8}+1=252\) số.
- Số các số chia 8 dư 1 trong dãy trên là: \(\dfrac{2009-1}{8}+1=252\) số.
Tương tự với các trường hợp số dư khác.
- Chia các số trong dãy thành 3 nhóm:
+ Nhóm 1: Gồm các số chia hết cho 8.
\(\Rightarrow\)Có 252 số trong nhóm 1.
+ Nhóm 2: Gồm các số chia 8 dư 1,2,3.
\(\Rightarrow\)Có \(252.3=756\) số trong nhóm 2.
+ Nhóm 3: Gồm các số chia 8 dư 4.
\(\Rightarrow\)Có 252 số trong nhóm 1.
+ Nhóm 4: Gồm các số chia 8 dư 5,6,7.
\(\Rightarrow\)Có \(252.3=756\) số trong nhóm 4.
- Để thỏa mãn yêu cầu đề bài, ta chỉ lấy 1 số trong nhóm 1 và 3 ; còn đối với nhóm 3 và 4, ta chỉ có thể lấy hết số trong 1 nhóm, chứ không thể lấy thêm số trong nhóm kia.
\(\Rightarrow\)Ta có thể lấy nhiều nhất \(1+1+756=758\) số (hay quân bài) để thỏa mãn yêu cầu đề bài.