Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\sqrt{\left(2x-1\right)^2}=3\)
\(\Leftrightarrow\left|2x-1\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=3\\2x-1=-3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x=4\\2x=-2\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
b) \(\dfrac{5}{3}\sqrt{15x}-\sqrt{15x}-2=\dfrac{1}{3}\sqrt{15x}\)
\(\Leftrightarrow\dfrac{5}{3}\sqrt{15x}-\sqrt{15x}-\dfrac{1}{3}\sqrt{15x}=2\)
\(\Leftrightarrow\dfrac{1}{3}\sqrt{15x}=2\)
\(\Leftrightarrow\sqrt{15x}=6\)
\(\Leftrightarrow15x=6^2\Leftrightarrow15x=36\)
\(\Rightarrow x=\dfrac{5}{12}\)

\(\sqrt{16x+16}-\sqrt{9x+9}+\sqrt{4x+4}+\sqrt{x+1}=16\)
\(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}=16\)
\(\Leftrightarrow4\sqrt{x+1}=16\)
\(\Leftrightarrow\sqrt{x+1}=4\)
<=> x + 1 = 16
<=> x = 15 (nhận)
~ ~ ~
\(\sqrt{4x+20}-3\sqrt{5+x}+\dfrac{4}{3}\sqrt{9x+45}=6\)
\(\Leftrightarrow2\sqrt{x+5}-3\sqrt{x+5}+4\sqrt{x+5}=6\)
\(\Leftrightarrow3\sqrt{x+5}=6\)
\(\Leftrightarrow\sqrt{x+5}=2\)
<=> x + 5 = 4
<=> x = - 1 (nhận)

\(ĐK:x\ge0\\ PT\Leftrightarrow\dfrac{5}{3}\sqrt{15x}-\sqrt{15x}-\dfrac{1}{3}\sqrt{15x}=2\\ \Leftrightarrow\sqrt{15x}\left(\dfrac{5}{3}-1-\dfrac{1}{3}\right)=2\\ \Leftrightarrow\dfrac{1}{3}\sqrt{15x}=2\Leftrightarrow\sqrt{15x}=6\Leftrightarrow15x=36\\ \Leftrightarrow x=\dfrac{12}{5}\left(tm\right)\)

\(ĐK:x\ge0\\ PT\Leftrightarrow\dfrac{2}{3}\sqrt{15x}-\dfrac{1}{3}\sqrt{15x}=2\\ \Leftrightarrow\dfrac{1}{3}\sqrt{15x}=2\Leftrightarrow\sqrt{15x}=6\\ \Leftrightarrow15x=36\Leftrightarrow x=\dfrac{12}{5}\left(tm\right)\)

\(M=\sqrt{15x^2-8x\sqrt{15+16}}\)
\(\Leftrightarrow M=\sqrt{\left(\sqrt{15}.x+4\right)^2}=\left|\sqrt{15}.x+4\right|=\sqrt{15}.x+4\)
Thay \(x=\sqrt{\dfrac{3}{5}}+\sqrt{\dfrac{5}{3}}\) vào BT ta được:
\(M=\sqrt{15}.\left(\sqrt{\dfrac{3}{5}}+\sqrt{\dfrac{5}{3}}\right)+4=\sqrt{9}+\sqrt{25}+4=3+5+4=12\)
Vậy \(M=12\)

Cho hình vuông ABCD, M là trung điểm AB. Trên tia đối của tia CB vẽ CN=AM. I là trung điểm MN. Tia DI cắt BC tại E, MN cắt CD tại F. Từ M vẽ MK vuông góc với AB và cắt DE tại K.
a, Cm MKNE là hình thoi (đã làm được)
b, Cm A,I,C thẳng hàng
c, Cho AB=a. Tính diện tích BMEtheo a (Đã làm được)
Giải Giùm mình đi, nhất là câu b
@Trương Thanh Nhân ơi !!! Bn có thể gửi câu hỏi đc mak !!!
Ko cần làm thế này đâu nhé !!!!

3.
Ta có: \(VT=\)\(8+2\sqrt{10+2\sqrt{5}}+8-2\sqrt{10+2\sqrt{5}}\)
\(=8+8+\left(2\sqrt{10+2\sqrt{5}}-2\sqrt{10+2\sqrt{5}}\right)\)
\(=16\ne VP\)
⇒ Đề sai
1. Ta có: \(\sqrt{4x}\)- 3\(\sqrt{x}\)+2\(\sqrt{15x}\)=18
⇌2\(\sqrt{x}\)-3\(\sqrt{x}\) +2\(\sqrt{15x}\)=18
⇌\(-\sqrt{x}\) +2\(\sqrt{15x}\)-15 = 3
⇌-(\(\sqrt{x}\) -2\(\sqrt{15x}\)+15 )=3
⇌(\(\sqrt{x}\)-\(\sqrt{15}\))=-3 (vô lí)
Vậy không tìm được giá trị x thỏa mãn bài toán
2.Ta có: B=\(\dfrac{1}{\sqrt{11-2\sqrt{30}}}-\dfrac{3}{7-2\sqrt{10}}\)
= \(\dfrac{1}{\sqrt{6-2\sqrt{6.5}+5}}-\dfrac{3}{2-2\sqrt{2.5}+5}\)
=\(\dfrac{1}{\sqrt{\left(\sqrt{6}-\sqrt{5}\right)^2}}-\dfrac{3}{\left(\sqrt{3}-\sqrt{2}\right)^2}\)
=\(\dfrac{1}{\sqrt{6}-\sqrt{5}}-\dfrac{3}{\sqrt{3}-\sqrt{2}}\)
hình như đề sai

\(\sqrt[3]{x+1}=x^3-15x^2+75x-125-6=0\)
\(\Leftrightarrow\sqrt[3]{x+1}+6=\left(x-5\right)^3\)
Đặt \(\sqrt[3]{x+1}=a-5\) ta được hệ:
\(\left\{{}\begin{matrix}\left(a-5\right)^3=x+1\\a-5+6=\left(x-5\right)^3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left(a-5\right)^3=x+1\\\left(x-5\right)^3=a+1\end{matrix}\right.\)
Trừ vế cho vế ta được:
\(\left(x-5\right)^3-\left(a-5\right)^3=a-x\)
\(\Leftrightarrow\left(x-a\right)\left(\left(x-5\right)^2+\left(x-5\right)\left(a-5\right)+\left(a-5\right)^2\right)+\left(x-a\right)=0\)
\(\Leftrightarrow\left(x-a\right)\left[\left(x-5+\frac{a-5}{2}\right)^2+\frac{3\left(a-5\right)^2}{4}+1\right]=0\)
\(\Leftrightarrow x-a=0\) (phần ngoạc phía sau luôn dương)
\(\Leftrightarrow x=a\Leftrightarrow x=\sqrt[3]{x+1}+5\Leftrightarrow x-5=\sqrt[3]{x+1}\)
\(\Leftrightarrow x^3-15x^2+75x-125=x+1\)
\(\Leftrightarrow x^3-15x^2+74x-126=0\)
\(\Rightarrow x=7\)

\(-2x^2+15x-5=\sqrt{2x^2-15x+11}\)
\(pt\Leftrightarrow-2x^2+15x-7=\sqrt{2x^2-15x+11}-2\)
\(\Leftrightarrow-\left(x-7\right)\left(2x-1\right)=\dfrac{2x^2-15x+11-4}{\sqrt{2x^2-15x+11}+2}\)
\(\Leftrightarrow-\left(x-7\right)\left(2x-1\right)-\dfrac{\left(x-7\right)\left(2x-1\right)}{\sqrt{2x^2-15x+11}+2}=0\)
\(\Leftrightarrow-\left(x-7\right)\left(2x-1\right)\left(1+\dfrac{1}{\sqrt{2x^2-15x+11}+2}\right)=0\)
Dễ thấy:\(1+\dfrac{1}{\sqrt{2x^2-15x+11}+2}>0\)
\(\Rightarrow\left[{}\begin{matrix}x-7=0\\2x-1=0\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=7\\x=\dfrac{1}{2}\end{matrix}\right.\)
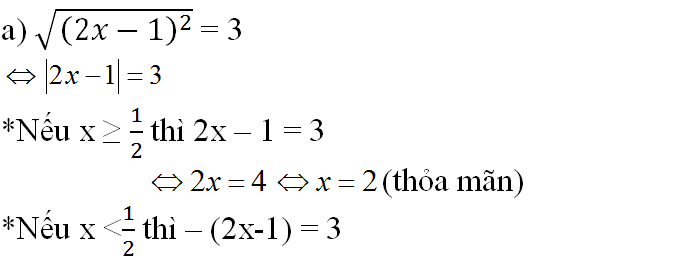
pt j ạ
Đặt \(\sqrt{15x}=a\)
Pt sẽ là \(\dfrac{5}{3a}-a+11=\dfrac{1}{3a}\)
=>\(\dfrac{4}{3a}=a-11\)
\(\Leftrightarrow3a^2-33a-4=0\)
=>\(a=11.12\)
=>căn 15x=11,12
=>15x=123,6544
hay \(x\simeq8,24\)