Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
\(=\left(\dfrac{x}{x+3}-\dfrac{x^2+9}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{3x+1}{x\left(x-3\right)}-\dfrac{1}{x}\right)\)
\(=\left(\dfrac{x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{x^2+9}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{3x+1}{x\left(x-3\right)}-\dfrac{x-3}{x\left(x-3\right)}\right)\)
\(=\left(\dfrac{x^2-3x-x^2-9}{\left(x+3\right)\left(x-3\right)}\right):\left(\dfrac{3x+1-x+3}{x\left(x-3\right)}\right)\)
\(=\dfrac{-3\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}:\dfrac{2x+4}{x\left(x-3\right)}\)
\(=\dfrac{-3}{\left(x-3\right)}\cdot\dfrac{x\left(x-3\right)}{2x+4}\\ =\dfrac{-3x}{2x+4}\)
b)
với `x=-1/2` (tmđk) ta có
\(\dfrac{-3\cdot\left(\dfrac{-1}{2}\right)}{2\cdot\left(-\dfrac{1}{2}\right)+4}=\dfrac{1}{2}\)
c)
để P=x thì
\(\dfrac{-3x}{2x+4}=x\)
\(=>-3x=\left(2x+4\right)\cdot x\)
\(-3x=2x^2+4x\)
\(2x^2+4x+3x=0\)
\(2x^2+7x=0\)
\(x\left(2x+7\right)=0\)
\(=>\left[{}\begin{matrix}x=0\\2x+7=0\end{matrix}\right.=>\left[{}\begin{matrix}x=0\left(loại\right)\\x=-\dfrac{7}{2}\left(tm\right)\end{matrix}\right.\)
d)
mik ko bt lm=)

Em tách ra mỗi lần hỏi đăng 1-3 bài thôi để nhận hỗ trợ sớm nhất nha em!



a) Xét \(\Delta BCD\) và \(\Delta HCB\) có
\(\widehat{BCD}:chung;\widehat{CBD}=\widehat{CHB}=90^o\)
=> \(\Delta BCD\) ~ \(\Delta HCB\)
=>\(\frac{BC}{HC}=\frac{CD}{BC}=BC^2=CH.CD\)
b( Xét \(\Delta BCD\) vuông tại B có "
\(CD^2=BC^2+BD^2=15^2+20^2=625\Rightarrow CD=25cm\)
Có \(\frac{BC}{HC}=\frac{CD}{BC}=BC^2=CH.CD\Rightarrow CH=9cm\)

a) Đặt: \(y-5=t\)
\(pt\Leftrightarrow\left(t-\frac{1}{2}\right)^4+\left(t+\frac{1}{2}\right)^4=0\)
\(\Leftrightarrow\left(t^2-t+\frac{1}{4}\right)\left(t^2-t+\frac{1}{4}\right)+\left(t^2+t+\frac{1}{4}\right)\left(t^2+t+\frac{1}{4}\right)=0\)
\(\Leftrightarrow\left(t^4-2t^3+\frac{3}{2}t^2-\frac{1}{2}t+\frac{1}{16}\right)+\left(t^4+2t^3+\frac{3}{2}t^2+\frac{1}{2}t+\frac{1}{16}\right)=0\)
\(\Leftrightarrow2t^4+3t^2+\frac{1}{8}=0\)
\(t^2=a\ge0\)
Giải tiếp pt ẩn a

\(\Leftrightarrow4x+3\le4x^2+4\Leftrightarrow4x^2-4x+1\ge0\)
\(\Leftrightarrow\left(2x-1\right)^2\ge0\) (Luôn đúng )
=> Đpcm
\(\frac{4x+3}{x^2+1}\le4\)
\(\Leftrightarrow\frac{4x+3}{x^2+1}\le\frac{4\left(x^2+1\right)}{x^2+1}\)
\(\Leftrightarrow4x+3\le4\left(x^2+1\right)\)
\(\Leftrightarrow4x+3\le4x^2+4\)
\(\Leftrightarrow4x-4x^2+3-4\le0\)
\(\Leftrightarrow-\left(2x-1\right)^2\le0\)(đpcm)

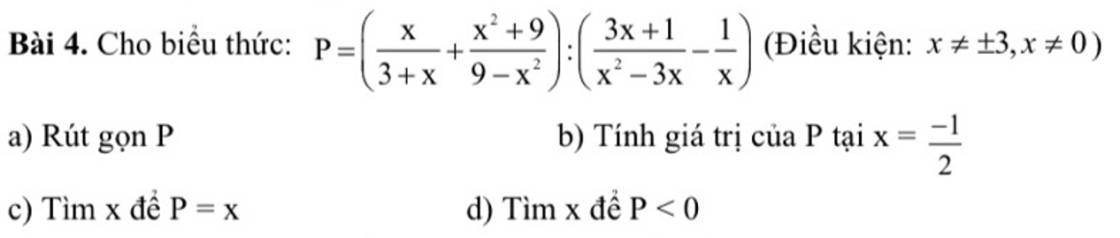


Shizuka kcj :)
(y - 4,5)4 + (y - 5,5)4 - 1 = 0
\(\Leftrightarrow\) 2y4 - 40y3 + 303y2 - 1030y + 1324,125 = 0
\(\Leftrightarrow\) 2y3 - 31y2 + 163,5y - 294,25 \(\approx\) 0
\(\Leftrightarrow\) 2y2 - 20y + 53,5 \(\approx\) 0
\(\Leftrightarrow\) y \(\approx\) \(\frac{9}{2}\); y \(\approx\) \(\frac{11}{2}\)
Vậy S = {\(\frac{9}{2}\); \(\frac{11}{2}\)}
Chúc bn học tốt!! (Bài này ko thể dùng dấu = được, phải dùng xấp xỉ nên mk phải dùng máy để tìm y, thông cảm )
)