
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



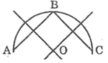
Lấy ba điểm A, B, C phân biệt trên đường viền.
Dựng đường trung trực của AB và BC. Hai đường trung trực cắt nhau tại O.
OA, OB, OC chính là bán kính của đường viền.

– Dòng thứ nhất: Vì d < R nên đường thẳng cắt đường tròn.
– Dòng thứ hai: Vì đường thẳng tiếp xúc với đường tròn nên d=R=6cm.
– Dòng thứ ba: Vì d>R nên đường thẳng và đường tròn không giao nhau.


Gọi MN = 2R là đường kính của đường tròn có cung tròn là ![]()
Theo bài tập 23, ta có:
KA. KB = KM. KN
hay KA. KB = KM. (2R - KM)
Thay số, ta có:
20. 20 = 3(2R - 3)
do đó 6R = 400 + 9 = 4099.
Vậy R = ≈688,2(mét)

Ta có: ΔO'AC cân tại O'
nên \(\widehat{CO'A}=180^0-2\cdot\widehat{A}\)(1)
Ta có: ΔOBA cân tại O
nên \(\widehat{BOA}=180^0-2\cdot\widehat{A}\)(2)
Từ (1) và (2) suy ra \(\widehat{CO'A}=\widehat{BOA}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên O'C//OB