

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



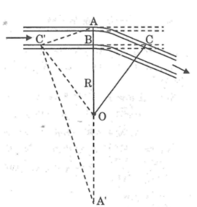
Xem đoạn đường ray thẳng là tiếp tuyến của hai đoạn đường ray vòng cung .
Điểm B cố định nằm trong đường tròn có cung là AC .Đường thẳng OB cắt đường tròn đó tại hai điểm A và A’
Ta có : A và A’ cố định
Vì B là tiếp điểm cung nhỏ trong nên BC là tiếp tuyến của đường tròn (O;OB)
Suy ra : BC ⊥ OB
Kéo dài BC cắt đường tròn (O;OA) tại C’
Suy ra : BC = BC’ ( đường kính vuông góc với dây cung)
Xét hai tam giác BAC và BC’A’ ta có:
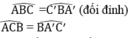
(hai góc nội tiếp cùng chắn cung AC)
Suy ra ∆ BAC đồng dạng ∆ BC’A’
⇔ BC'/AB =BA'/BC ⇒ BC.BC’ = AB.A’B
Mà BC = BC’ và BA’ = 2R – AB
Nên B C 2 = AB(2R –AB)
⇔ 28 , 4 2 =1,1 (2R – 1,1)
⇔ 2,2R =806,56 + 1,21 =807,77
⇔ R = 807,77 : 2,2 ≈ 367,2(m)
Vậy bán kính đoạn đường ray hình vòng cung là 367,2m


Gọi MN = 2R là đường kính của đường tròn có cung tròn là ![]()
Theo bài tập 23, ta có:
KA. KB = KM. KN
hay KA. KB = KM. (2R - KM)
Thay số, ta có:
20. 20 = 3(2R - 3)
do đó 6R = 400 + 9 = 4099.
Vậy R = ≈688,2(mét)

Hướng dẫn giải:
∆OAB là tam giác đều có cạnh bằng R = 5,1cm. Áp dụng công thức tính diện tích tam giác đều cạnh a là a2√44 ta có
S∆OBC = SΔOBC=R2√34 (1)
Diện tích hình quạt tròn AOB là:
π.R2.6003600=πR26 (2)
Từ (1) và (2) suy ra diện tích hình viên phân là:
πR26−R2√34=R2(π6−√34)
Thay R = 5,1 ta có Sviên phân ≈ 2,4 (cm2)

a) Diện tích xung quanh của hình trụ : \(288\pi\left(cm^2\right)\)
b) Thể tích hình cầu : \(2304\pi\left(cm^3\right)\)
c) Diện tích mặt cầu : \(576\pi\left(cm^2\right)\)