Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có điểm A có tọa độ xA = 2, yA = 1
Vì điểm A thuộc đồ thị hàm số y = ax nên ta có:
1 = a.2 => a = \(\dfrac{1}{2}\)
Vậy hệ số a bằng \(\dfrac{1}{2}\), ta có hàm số y = \(\dfrac{1}{2}x\)
b) Lúc này đường thẳng OA là đồ thị của hàm số y = \(\dfrac{1}{2}x\)
Khi x = \(\dfrac{1}{2}\) thì y = \(\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{4}\)
Ta có điểm B trên đồ thị có tọa độ B(\(\dfrac{1}{2};\dfrac{1}{4}\))
c) Thay y = -1 vào hàm số y = \(\dfrac{1}{2}x\), ta có:
-1 = \(\dfrac{1}{2}x\) => x = -2
Khi đó điểm C trên đồ thị có tọa độ C(-2; -1)
a) Vì A(2;1) thuộc đồ thị của hàm số y= ax nên thay x = 2 ; y = 1 vào công thức y=ax . Ta có :

b) Từ điểm 1/2= a.2 ⇒ a =1/2
trên trục hoành vẽ đường thẳng song song trục tung cắt đồ thị tại điểm B. B là điểm cần đánh dấu. c) Từ điểm -1 trên trục tung vẽ đường thẳng song song với trục hoành cắt đồ thị tại điểm C. C là điểm cần đánh dấu.

Hướng dẫn làm bài:
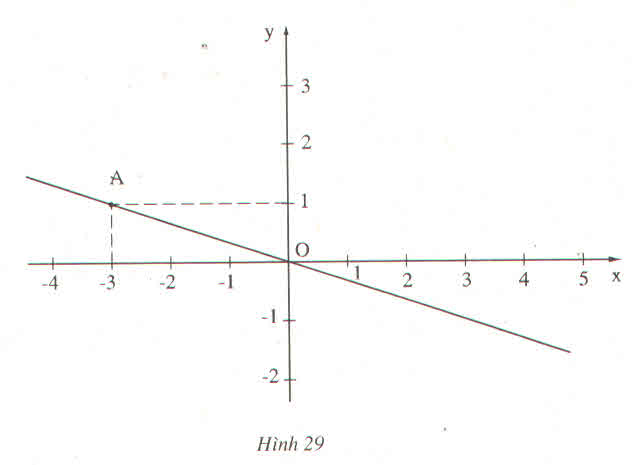
Ta có hàm số y = ax có đồ thị là đường thẳng qua điểm A(-3;1) nên ta có:
x = - 3 thì y = 1
Suy ra: 1 = a. (-3)
⇒a=−13⇒a=−13.
Vậy ⇒a=−13⇒a=−13. .
Trên hình vẽ ta thấy x=-3, y=1
\(\Rightarrow1=-3a\Rightarrow a=\dfrac{-1}{3}\)

1. đề bạn ghi rõ lại giúp mình đc ko r mình giải lại cho
2. Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{2x^2}{2.3^2}=\dfrac{y^2}{5^2}=\dfrac{2x^2-y^2}{18-25}=\dfrac{-28}{-7}=4\)
\(\dfrac{x}{3}=4\Rightarrow x=12\)
\(\dfrac{y}{5}=4\Rightarrow y=20\)
Vậy x=12 và y=20

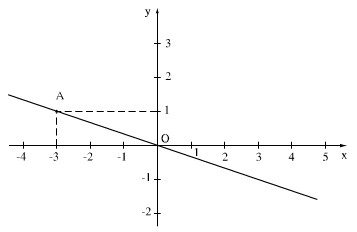
a)Thay B(-2; -1) vào hàm số y = bx, ta có: 1=−2.b⇒b=−121=−2.b⇒b=−12
Vậy b=−12b=−12.
b) c) Hình dưới.
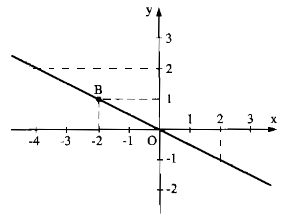

Bài 2:
a) Ta có : Từ \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
\(\Rightarrow\dfrac{5a}{5c}=\dfrac{7b}{7d}\)
Theo tính chất dãy tỉ số bằng nhau, ta có :
\(\dfrac{5a}{5c}=\dfrac{7b}{7d}=\dfrac{5a+7b}{5c+7d}\left(1\right)\)
Và \(\dfrac{5a}{5c}=\dfrac{7b}{7d}=\dfrac{5a-7b}{5c-7d}\left(2\right)\)
Từ (1) và (2)=> \(\dfrac{5a+7b}{5c+7d}=\dfrac{5a-7b}{5c-7d}\Rightarrow\dfrac{5a+7b}{5a-7b}=\dfrac{5c+7d}{5c-7d}\)Vậy...
b) Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Thay các đẳng thức vừa tìm được , ta có :
\(\dfrac{ac}{bd}=\dfrac{bk.dk}{bd}=k^2\left(1\right)\)
\(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}\)
\(=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\left(2\right)\)
từ (1) và (2)=> đpcm
tik mik nha !!!
1. Bạn xem lại đề bài nhé! Mình nghĩ là \(2x=3y=5z\) thì đúng hơn!
2.
a) Ta có: \(\dfrac{a}{b}=\dfrac{c}{d}\)
\(\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
\(\Rightarrow\dfrac{5a}{5c}=\dfrac{7b}{7d}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{5a}{5c}=\dfrac{7b}{7d}=\dfrac{5a+7b}{5c+7d}=\dfrac{5a-7b}{5c-7d}\)
Từ \(\dfrac{5a+7b}{5c+7d}=\dfrac{5a-7b}{5c-7d}\Rightarrow\dfrac{5a+7b}{5a-7b}=\dfrac{5c+7d}{5c-7d}\)(đpcm)
Vậy \(\dfrac{5a+7b}{5a-7b}=\dfrac{5c+7d}{5c-7d}\)
b) Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Rightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có:
\(VT=\dfrac{ac}{bd}=\dfrac{bk.dk}{bd}=\dfrac{bd.k^2}{bd}=k^2\left(1\right)\)
\(VP=\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{b^2.k^2+d^2.k^2}{b^2+d^2}=\dfrac{k^2.\left(b^2+d^2\right)}{b^2+d^2}=k^2\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\)
\(\Rightarrow\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\left(đpcm\right)\)
Vậy \(\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\)

Kêu người ta giúp mà ói vào mặt người ta vậy à?
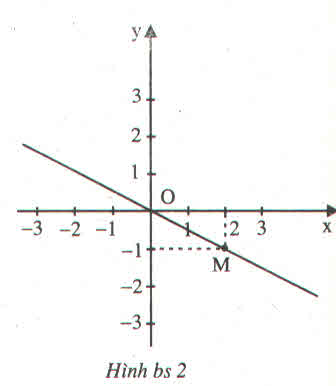


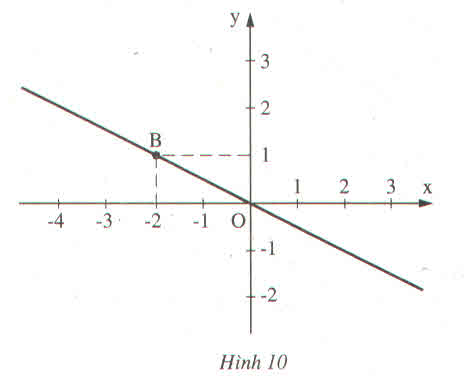
kết quả là (D) y= -1/2x
(A)