Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tính chiều cao của bức tường(h.129) biết rằng chiều cao của thang là 4m và chân thang cách tường 1m.


Theo định li pytago, ta có:
AC2+ BC2=AB2
nên AC2=AB2+BC2
Suy ra LAD= √15 ≈ 3.87

Hình a)
Áp dụng định lí Pytago, Ta có:
x2 =122+5 = 144+25=169
=> 132=x2 => x=13.
Hình b) ta có:
x2= 12 + 22 = 1+4=5
x= √5
Hình c)
Theo định lí pytago:
292=212+x2
nên x2=292-212
= 841-441=400=202
=>x=20
Hình d)
x2=( √7)2+32=7+9=16=42
=>x=4.

(-10/3)5.(-6/5)4=-100000/243.1296/625=-853,(3)
K CHO MÌNH NHA CẢM ƠN
\(\left(\frac{-10}{3}\right)^5x\left(\frac{-6}{5}\right)^4\)
\(=\frac{-100000}{243}x\frac{1296}{625}\)
\(=\frac{-2560}{3}\)
Cố lên!!!

chiều cao AB là
\(\sqrt{8,5^2-7,5^2}=\sqrt{72,25-56,25}=\sqrt{16}=4\)
vậy chiều cao AB là 4m

d) \(\dfrac{2}{3}-\left[\left(\dfrac{-7}{4}\right)-\left(\dfrac{1}{2}+\dfrac{3}{8}\right)\right]\)
\(=\dfrac{2}{3}-\left[\left(\dfrac{-7}{4}\right)-\left(\dfrac{4}{8}+\dfrac{3}{8}\right)\right]\)
\(=\dfrac{2}{3}-\left[\left(\dfrac{-14}{8}-\dfrac{7}{8}\right)\right]=\dfrac{2}{3}-\left(\dfrac{-21}{8}\right)\)
\(=\dfrac{16}{24}+\dfrac{63}{24}=\dfrac{79}{24}\)
Hok tốt

a) \(\dfrac{16}{2^n}=2\Rightarrow2^n=\dfrac{16}{2}=8=2^3\)
\(\Rightarrow n=3\)
b) \(\dfrac{\left(-3\right)^n}{81}=-27\)
\(\Leftrightarrow\dfrac{\left(-3\right)^n}{3^4}=\left(-3\right)^3\)
\(\Leftrightarrow\left(-3\right)^n=-\left(3^4\cdot3^3\right)=\left(-3\right)^7\)
\(\Rightarrow n=7\)
c) \(8^n:2^n=4\)
\(\Leftrightarrow2^{3n}:2^n=2^2\)
\(\Leftrightarrow3n-n=2\)
\(\Leftrightarrow2n=2\Rightarrow n=1\)
a, \(\dfrac{16}{2^n}=2\Rightarrow2^n.2=16\Rightarrow2^{n+1}=2^4\Rightarrow n+1=4\Rightarrow n=3\). Vậy n=3.
b, \(\dfrac{\left(-3\right)^n}{81}=-27\Rightarrow\left(-3\right)^n=81.\left(-27\right)\Rightarrow\left(-3\right)^n=-2187\)
\(\Rightarrow\left(-3\right)^n=\left(-3\right)^7\Rightarrow n=7\)
Vậy n=7
c, \(8^n:2^n=4\Rightarrow\left(2^3\right)^n:2^n=2^2\Rightarrow2^{3n}:2^n=2^2\Rightarrow2^{2n}=2^2\Rightarrow2n=2\Rightarrow n=1\)
Vậy n=1.

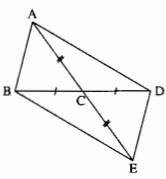
Giải
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)
A B C D E
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)

a) \(\frac{16}{2^n}=2\)
\(\Rightarrow16=2\cdot2^n\)
\(\Rightarrow16=2^{n+1}\)
\(\Rightarrow2^4=2^{n+1}\)
\(\Rightarrow n+1=4\)
\(\Rightarrow n=4-1\)
\(\Rightarrow n=3\)
Vậy n=3
b) \(\frac{\left(-3\right)^n}{81}=-27\)
\(\Rightarrow\left(-3\right)^n=-27\cdot81\)
\(\Rightarrow\left(-3\right)^n=\left(-3\right)^3.\left(-3\right)^4\)
\(\Rightarrow\left(-3\right)^n=\left(-3\right)^7\)
\(\Rightarrow n=7\)
Vậy n=7
c ) \(8^n:2^n=4\)
\(\Rightarrow2^{3n}:2^n=2^2\)
\(\Rightarrow2^{2n}=2^2\)
\(\Rightarrow2n=2\)
\(\Rightarrow n=2:2\)
\(\Rightarrow n=1\)
Vậy n=1


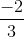
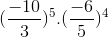
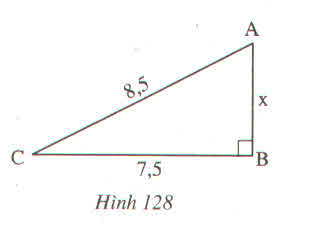
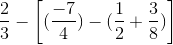
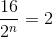
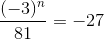
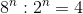
Theo định li py-ta-go cho tam giá ABC vuông tại B:
AB2 + BC2 = AC2
=> AB2 = AC2 – BC2 = 8,52 - 7,52 = 72,5 - 56,5 = 16
Vậy AB = 4
bạn làm sai ở chỗ AB^2 +BC^=AC^2
sửa là : CA^2 +CB^2= AB^2 .