Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì con kiến phải bò theo mặt của hình hộp từ Q đến P tức phải bò trên "một mặt phẳng". Ta vẽ hình khai triển của hình hộp chữ nhật và trải phẳng như sau:
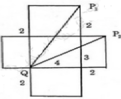
Khi đó, P sẽ có hai vị trí là P1 và P2. Và quãng đường ngắn nhất sẽ là một trong hai đoạn thẳng QP1 hoặc QP2.


Trải 6 mặt của hình lập phương ABCD.A'B'C'D' . Để đi đường ngắn nhất từ M đến M' ( M' chính là trung điểm của A'D' trên mặt khai triển ) thì con kiến cần bò theo đoạn thẳng MM' . Trên chiếc hộp , đường đi ngắn nhất của con kiến là đường MNPQKZM ( dễ thấy N , P ,Q , K , Z lần lượt là trung điểm của DD' , CD , BC , BB' , A'B' )

\(S_{XQ}=\left(4+6\right)\cdot2\cdot3=60\left(cm^2\right)\)
\(S_{TP}=60+24\cdot2=108\left(cm^2\right)\)

Thể tích hình hộp chữ nhật là V1 = 5.5.3 = 75
Vì OI = IJ , IJ = AA' = 3 và SJ = 9 nên OI = 3 và SO = 3
\(\Rightarrow A_1B_1C_1D_1\) là hình vuông cạnh 2,5
Vậy thể tích hình chóp S.A1B1C1D1 là :
\(V_2=\dfrac{1}{3}.3.2,5.2,5=6,25\)
Thể tích hình chóp S.A'B'C'D' là :
\(V_3=\dfrac{1}{3}.6.5.5=50\)
Vậy thể tích cần tính là : \(V=V_1+V_3-V_2=118,75\)

| l | 25 | 8 | 15 | 8 |
| v | 20 | 4 | 12 | 6 |
| h | 10 | 6 | 4 | 12 |
| Sxq | 900 | 144 | 216 | 336 |
| Stp | 1900 | 208 | 576 | 432 |
| V | 5000 | 192 | 720 | 576 |

a. Ba đường thẳng CG, HG, FG cắt nhau tại G.
b. Mặt phẳng (ABFE) và mặt phẳng (BCGF) cắt nhau theo đường thẳng BF.
c. Mặt phẳng (EFBA) và mặt phẳng (FGCB) cắt nhau theo đường thẳng BF.

c) Mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).
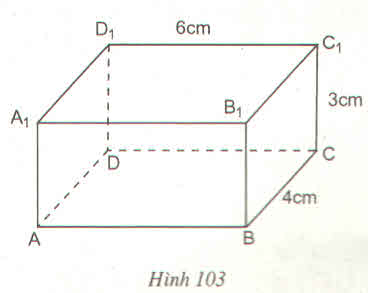
a) Ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD.
b) Cạnh CD song song với hai mặt phẳng (ABEF) và (EFGH).
c) Mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).
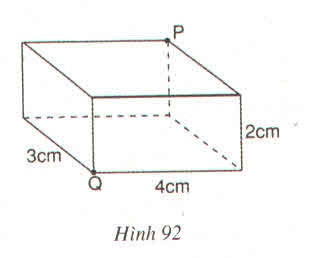










Vì con kiến phải bò theo mặt của hình hộp từ Q đến P tức phải bò trên "một mặt phẳng". Ta vẽ hình khai triển của hình hộp chữ nhật và trải phẳng như sau:
Khi đó, P sẽ có hai vị trí là P1 và P2. Và quãng đường ngắn nhất sẽ là một trong hai đoạn thẳng QP1 hoặc QP2.
Cô giáo tớ bảo thế là không được !!!!!