Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

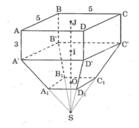
Thể tích phần hình hộp chữ nhật:
V = 5.5.5 = 75 (đvtt)
Ta có: IJ = AA' ⇒ IJ = 3
OI = IJ = 3
SJ = 9 ⇒ SO = 3
Suy ra: S A 1 = A 1 A ' ; S D 1 = D 1 D '
Khi đó hình vuông A 1 B 1 C 1 D 1 có cạnh A 1 B 1 = 1/2 A'B' = 2,5
Thể tích hình chóp đều S. A'B'C'D' là:
V= 1/3 (5.5).6 = 50 (đvtt)
Thể tích hình chóp đều A 1 B 1 C 1 D 1 là:
V= 1/3(2,5.2,5).3 = 6,25 (đvtt)
Thể tích hình chóp cụt A'B'C'D'. A 1 B 1 C 1 D 1 là:
V = 50 – 6,25 = 43,75 (đvtt)
Thể tích của một trụ bê tông là:
V = 43,75 + 75 = 118,75 (đvtt).

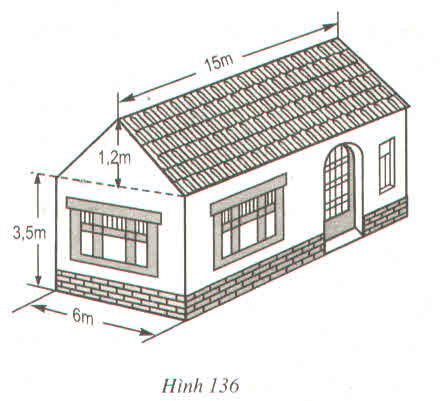
Thể tích lăng trụ là:
\(V=\dfrac{1}{2}\cdot6\cdot1.2\cdot15=54\left(m^3\right)\)
Thể tích hình hộp chữ nhật là:
\(V=6\cdot15\cdot3.5=315\left(m^3\right)\)
Thể tích của cả hình là:
315+54=369(m3)

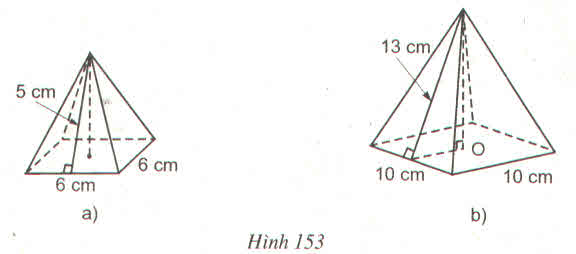
V = \(\dfrac{1}{3}\)S . h = \(\dfrac{1}{3}\)a.h.h = \(\dfrac{1}{3}\)ah2

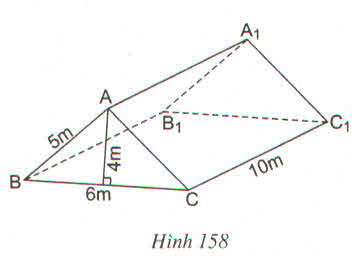
Diện tích đáy ABC: S1= 1/2.6.4=12 (m2)
Diện tích mặt BCC1B1: S2=6.10=60 (m2)
Diện tích AA1C1C: S3= 10.5=50 (m2)
Ta thấy hai mặt AA1B1B và AA1C1C bằng nhau nên:
Stp= 2S1+S2+2S3= 2.12+60+2.50= 184 (m2)

\(S_{XQ}=\left(4+6\right)\cdot2\cdot3=60\left(cm^2\right)\)
\(S_{TP}=60+24\cdot2=108\left(cm^2\right)\)

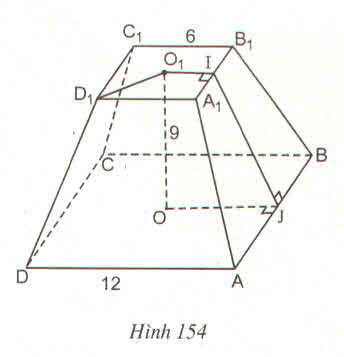







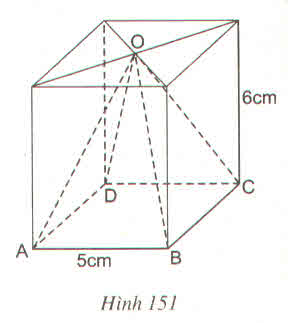
Thể tích hình hộp chữ nhật là V1 = 5.5.3 = 75
Vì OI = IJ , IJ = AA' = 3 và SJ = 9 nên OI = 3 và SO = 3
\(\Rightarrow A_1B_1C_1D_1\) là hình vuông cạnh 2,5
Vậy thể tích hình chóp S.A1B1C1D1 là :
\(V_2=\dfrac{1}{3}.3.2,5.2,5=6,25\)
Thể tích hình chóp S.A'B'C'D' là :
\(V_3=\dfrac{1}{3}.6.5.5=50\)
Vậy thể tích cần tính là : \(V=V_1+V_3-V_2=118,75\)
Sao suy ra được cạnh bằng 2.5 vậy bn