Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C K H
a) Vì \(\widehat{B}=\widehat{C}\)
=> \(\Delta ABC\) cân tại A
=> \(\widehat{B}\) và \(\widehat{C}\) cùng nhọn
b) Xét \(\Delta ABH\) và \(\Delta ACK\) có:
AB = AC (\(\Delta ABC\) cân)
\(\widehat{A}\left(chung\right)\)
\(\widehat{AHB}=\widehat{AKC}=90^0\)
Do đó: \(\Delta ABH=\Delta ACK\left(ch-gn\right)\)
=> BH = CK (hai cạnh tương ứng)

1) Ta có hình vẽ: O B D A C y x E 1 2 1 2 1 2 H 1 2
a) Ta có:
OC = OA + AC
OD = OB + BD
mà OA = OB ( gt)
AC = BD (gt)
suy ra OC = OD
Xét 2 tam giác OAD và tam giác OBC có:
OA = OB (gt)
OC = OD (cmt)
O là góc chung
suy ra tam giác OAD = tam giác OBC (c- g-c)
b) Ta có: góc A1 + góc A2 = 180 độ
góc B1 + góc B2 = 180 độ
Mà góc A1 = góc B1 ( vì tam giác OAD = tam giác OBC)
suy ra góc A2 = góc B2
Xét 2 tam giác EAC và tam giác EBD có:
AC = BD (gt)
góc C = góc D (vì tam giác OAD = tam giác OBC)
góc A2 = góc B2 ( cmt)
suy ra tam giác EAC = tam giác EBD)
c) Xét 2 tam giác OAE và tam giác OBE có:
OE là cạnh chung
OA = OB ( gt)
AE = BE (vì tam giác EAC = tam giác EBD)
suy ra tam giác OAE = tam giác OBE (c- c-c)
suy ra góc O1 = góc O2 (2 góc tương ứng)
suy ra OE là tia phân giác của góc xOy
Xét 2 tam giác OCH và tam giác ODH có:
góc O1 = O2 (cmt)
OH là cạnh chung
OC = OD (cmt ở câu a)
suy ra tam giác OCH = tam giác ODH (c-g-c)
suy ra góc H1 = góc H2 (2 góc tương ứng)
mà góc H1 + H2 = 180 độ
suy ra H1 = H2 = 180/2 = 90 độ
suy ra OH vuông góc với CD
Mình cm OH vuông góc với CD vì nếu bạn cho đề là OE vuông góc với CD thì không thể cm được, điểm E nằm như vậy ( theo hình vẽ) sao cm được! Bạn xem lại hộ mình nhé!

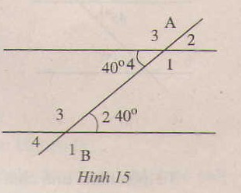
Xem hình bên rồi điền vào chỗ trồng (...) trong các câu sau:
a) và
là một cặp góc .so le trong ....
b) và
là một cặp góc ..đồng vị ..
c) và
là một cặp góc ..đồng vị ....
d) và
là một ..cặp góc so le trong..
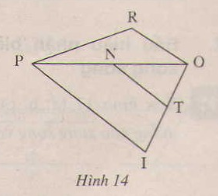
) Vẽ lại hình.
b) Ghi số đo ứng với các góc còn lại ta được hình bên:

c) Ta có:
Bài 21 : a) Góc IPO và góc POR là 1 cặp góc so le trong
b) góc OPI và góc TNO là 1 cặp góc đồng vị
c) góc PIO và góc NTO là 1 cặp góc đồng vị
d)góc OPR và góc POI là một cặp góc so le trong
cho tam giác , có góc A = 30 độ , dựng bên ngoài tam giác abc tam giác đều bcd . Chứng minh rằng =
+

Xét tam giác ABD và tam giác FBC có:
AB=FB ( cạnh tam giác đều FAB)
DB=BC ( cạnh tam giác đều DBC)
góc ABD = góc FBC ( cùng bằng góc ABC + 60 độ)
Suy ra tam giác ABD = tam giác FBC (c.g.c)
=> FC=AD
Chúc bạn học tốt !!
Nhớ tick cho mk nhé ....

Bn tự vẽ hình nha!!1
a) Xét \(\Delta AOB \) và \(\Delta COD\) có:
OA = OC (gt)
\(\widehat{AOB} = \widehat{COD}\) (đối đỉnh)
OB = OD (gt)
\(\Rightarrow\)\(\Delta AOB = \Delta COD (cgc)\)
b) Xét \(\Delta DKO\) và \(\Delta BHO\) có:
\(\widehat{DKO} = \widehat{BHO} = 90^0\)
OD = OB (gt)
\(\widehat{DOK} = \widehat{BOH}\) (đối đỉnh)
\(\Rightarrow\)\(\Delta DKO = \Delta BHO (ch-gn)\)
\(\Rightarrow DK=BH\) (2 cạnh tương ứng)
c) Vì \(\Delta AOB = \Delta COD (cmt)\)
\(\Rightarrow\)\(\widehat{ABO} = \widehat{CDO}\) (2 góc tương ứng)
Xét \(\Delta ODN\) và \(\Delta OBM\) có:
OD = OB (gt)
\(\widehat{ODN} = \widehat{OBM}\) (cmt)
DN = BM (gt)
\(\Rightarrow\)\(\Delta ODN = \Delta OBM (cgc)\)
\(\Rightarrow\)\(\widehat{DON} = \widehat{BOM}\) (2 góc tương ứng)
Ta có:
\(\widehat{BOM} + \widehat{MOD} =180^0\) (kề bù)
mà \(\widehat{DON} = \widehat{BOM}\) (cmt)
\(\Rightarrow\)\(\widehat{DON} + \widehat{MOD} =180^0\)
Lại có: \(\widehat{DON} + \widehat{MOD} =\widehat{MON}\)
\(\Rightarrow\)\(\widehat{MON} = 180^0\)
hay M, O , N thẳng hàng
a) Vì Bˆ=CˆB^=C^
=> ΔABCΔABC cân tại A
=> BˆB^ và CˆC^ cùng nhọn
b) Xét ΔABHΔABH và ΔACKΔACK có:
AB = AC (ΔABCΔABC cân)
Aˆ(chung)A^(chung)
AHBˆ=AKCˆ=900AHB^=AKC^=900
Do đó: ΔABH=ΔACK(ch−gn)ΔABH=ΔACK(ch−gn)
=> BH = CK (hai cạnh tương ứng)