Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt A=\(\dfrac{1}{21}+\dfrac{1}{22}+...+\dfrac{1}{60}\)
A=\(\left(\dfrac{20}{20.21}+\dfrac{21}{21.22}+...+\dfrac{39}{39.40}\right)+\left(\dfrac{40}{40.41}+\dfrac{41}{41.42}+...+\dfrac{59}{59.60}\right)\)
=>A >\(20\cdot\left(\dfrac{1}{20.21}+\dfrac{1}{21.22}+...+\dfrac{1}{39.40}\right)+40\cdot\left(\dfrac{1}{40.41}+\dfrac{1}{41.42}+...+\dfrac{1}{59.60}\right)\)
A>\(20\cdot\left(\dfrac{1}{20}-\dfrac{1}{40}\right)+40\cdot\left(\dfrac{1}{40}-\dfrac{1}{60}\right)=\dfrac{5}{6}>\dfrac{11}{15}\)
Mặt khác: A<\(40\cdot\left(\dfrac{1}{20.21}+\dfrac{1}{21.22}+...+\dfrac{1}{39.40}\right)+60\cdot\left(\dfrac{1}{40.41}+\dfrac{1}{41.42}+...+\dfrac{1}{59.60}\right)\)
A<\(40\cdot\left(\dfrac{1}{20}-\dfrac{1}{40}\right)+60\cdot\left(\dfrac{1}{40}-\dfrac{1}{60}\right)=\dfrac{3}{2}\)
Vậy...

bài 2
| a;đặt biểu thức là S | |
| S < 1/1.2 + 1/2.3 + .......1/(n-1)n | |
| = 1- 1/2 +1 /2 -1/3+........ + 1/n-1 - 1/n | |
|
= 1 -1/n <1 |
|
| vậy S < 1 | |

Câu hỏi của Nguyễn Hải Văn - Toán lớp 6 - Học toán với OnlineMath

Lời giải:
Ta có: \(n^2=n.n> (n-1)n\) với mọi \(n\geq 2\)
\(\Rightarrow \frac{1}{n^2}< \frac{1}{n(n-1)}\)
Do đó:
\(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{n^2}< \underbrace{\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{n(n-1)}}_{N}(1)\)
Lại có: \(N=\frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+...+\frac{n-(n-1)}{(n-1)n}\)
\(N=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{n-1}-\frac{1}{n}=1-\frac{1}{n}< 1(2)\)
Từ (1); (2) theo nguyên tắc bắc cầu suy ra:
\(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{n^2}< 1\)
Ta có đpcm.

a, \(1\dfrac{13}{15}.\left(0,5\right)^2.3+\left(\dfrac{8}{15}-1\dfrac{19}{60}\right):1\dfrac{23}{24}\)
= \(\dfrac{28}{15}.\dfrac{25}{100}.3+\left(\dfrac{8}{15}-\dfrac{79}{60}\right):\dfrac{47}{24}\)
= \(\dfrac{28}{15}.\dfrac{1}{4}.3+\left(\dfrac{32-79}{60}\right).\dfrac{24}{47}\)
= \(\dfrac{84}{60}+\dfrac{-47}{60}.\dfrac{24}{47}\)
= \(\dfrac{84}{60}+\dfrac{-24}{60}=\dfrac{60}{60}=1\)
b, \(\dfrac{\left(\dfrac{11^2}{200}+0,415\right):0,01}{\dfrac{1}{12}-37,25+3\dfrac{1}{6}}\)
= \(\dfrac{\left(\dfrac{121}{200}+\dfrac{415}{1000}\right):\dfrac{1}{100}}{\dfrac{1}{12}-\dfrac{3725}{100}+\dfrac{19}{6}}=\dfrac{\left(\dfrac{121}{200}+\dfrac{83}{200}\right).100}{\dfrac{1}{12}-\dfrac{149}{4}+\dfrac{19}{6}}\)
= \(\dfrac{\dfrac{51}{50}.100}{-34}=\dfrac{102}{-34}=-3\)

\(B=\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{21}+...+\dfrac{1}{120}\)
\(\Leftrightarrow B=\dfrac{2}{20}+\dfrac{2}{30}+\dfrac{2}{42}+...+\dfrac{2}{240}\)
\(\Leftrightarrow B=2\left(\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+...+\dfrac{1}{240}\right)\)
\(\Leftrightarrow B=2\left(\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{15.16}\right)\)
\(\Leftrightarrow B=2\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{15}-\dfrac{1}{16}\right)\)
\(\Leftrightarrow B=2\left(\dfrac{1}{4}-\dfrac{1}{16}\right)=\dfrac{3}{8}\)
Vì \(\dfrac{3}{8}< \dfrac{1}{2}\)
\(\Rightarrow B< \dfrac{1}{2}\left(ĐPCM\right)\)

\(\left(\dfrac{1}{5}-\dfrac{1}{6}-\dfrac{1}{30}\right).\left(\dfrac{21}{22}+\dfrac{22}{23}+...+\dfrac{102}{103}\right)\)
\(=0.\left(\dfrac{21}{22}+\dfrac{22}{23}+...+\dfrac{102}{103}\right)\)
\(=0\)
vì \(\dfrac{1}{5}-\dfrac{1}{6}-\dfrac{1}{30}\)=0 nên
(15−16−13015−16−130 ).(2122+2223+......+102103)=0
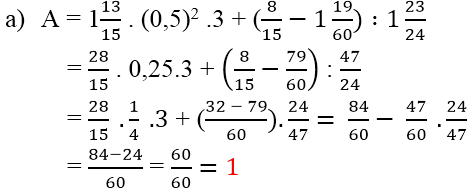
Bạn vào đây nhé! https://hoc24.vn/hoi-dap/question/206800.html
Câu hỏi giống nhau nên bạn vào link đó xem đỡ mất công mình ghi lại nhé!